Vincent GODARD
Département de Géographie
Université de Paris 8
V.1.9 - Dernière mise à jour : 27/02/2023
Fiche Mémo n°2.1. du cours de Cartographie niveau 2 :
Géodésie et projections
La Terre est une sphère
Les globes en sont l'unique
représentation fidèle
Mais pour des raisons
pratiques
on préfère utiliser des planisphères ou des mappemondes (désuet)
- Avantage
: se plient et se transportent partout même à grande échelle
- Inconvénient : les surfaces courbes qui ne peuvent y être représentées à
plat sans déformations
Pour passer d'une sphère à un plan on
va pratiquer une projection
Pour commencer, une petite vidéo de 26 min qui commence à être historique
(1999) : C'est pas sorcier - Cartographie
1. Les formes de la Terre
Les formes de la Terre s'étudient au
travers de la géodésie*
La géodésie est la science des formes et dimensions de la Terre et de
son champ de pesanteur.
1.1. La géodésie
- L'hypothèse d'une terre
sphérique remonte à l'antiquité.
C'est le savant grec Ératosthène vers 240 avant JC qui a
fait la première mesure du rayon de la Terre.
Précision de l'ordre de 10 p.100
Des cosmographes arabes reprendront cette mesure au IXe siècle.
fig. 1 - La mesure du rayon terrestre par
Ératosthène
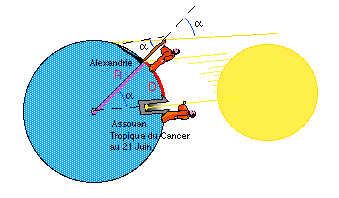
Sources : www.ign.fr
En 240 ans av. JC, Ératosthène a déterminé le premier rayon terrestre
en mesurant l'angle entre les verticales d'Assouan (Syène en grec
ancien francisé) et d'Alexandrie et la distance qui les sépare. Cette
méthode des arcs va être utilisée jusqu'au XVIIe siècle (cf.
Denis Guedj, 2003, Les cheveux de Bérénice. Le Seuil).
- Naissance de la géodésie moderne au XVIIe siècle.
Naissance rendue possible par :
- de nouvelles techniques => la
triangulation (voir triangulation et histoire de la triangulation)
;
- de nouveaux instruments => lunettes à réticules.
ces techniques donneront naissance à la première
carte de France sans déformations en 1745 (Cassini
III)
fig. 2 - Triangulation le long de la méridienne
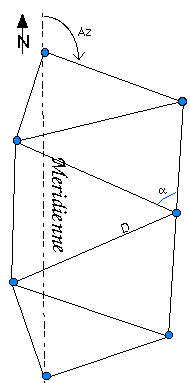
Sources : www.ign.fr
On peut voir comment dans ce film de l'IGN "De l'avion à la carte" datant des années 50,
comment sont :
- tracés les chaînes de triangles (triangulation) ;
- implantés les réseaux géodésiques de premier ordre et
les sous réseaux ;
- choisis les points géodésiques dans le paysage ;
- calculés les altitudes des repères de nivellement...
Comment calculer une distance à l'aide de la méthode des
triangles ? Ces deux vidéo vous disent tout :
Grâce à ces progrès, des physiciens comme Newton et
Huygens calculent l'aplatissement des pôles (dû à la rotation
terrestre).
- L'hypothèse d'une terre
légèrement aplatie selon l'axe des pôles
est démontrée du XVIIIe
siècle.
Deux théories s'affrontent :
- les "newtoniens" penchent pour une terre aplatie aux
pôles ;
- les "cassiniens" pour une terre aplatie à l'équateur.
- Qui va gagner ?
L’Académie des Sciences commandite des expéditions pour
mesurer des arcs de méridiens terrestres :
- une en Laponie => Maupertuis, Clairaut ;
- une au Pérou => la Condamine, Bouguer.
C'est la théorie de Newton qui triomphe => La Terre est aplatie aux pôles.
En 1799, l'Académie des Sciences (Delambre) choisit le
mètre comme unité de mesure universelle de longueur sur la base de 1
mètre = un quart de la 1 / 10 000 000 partie du méridien terrestre.
Naissance du système métrique (cf. Denis
Guedj, 2000, Le Mètre du monde. Le Seuil ; Ken Adler, 2002, Mesurer le
monde, l'incroyable histoire de l'invention du mètre. Champs Flammarion).
Mais en fait, c'est une succession de mesures de
méridiennes qui s'enchaînent en fonction des progrès techniques.
1. méridienne de Picard (1669-1671)
2. méridienne de Cassini (1683-1718)
3. triangulation de Cassini (1733-1770)
4. méridienne de France (1739-1740)
5. triangulation des Ingénieurs géographes (1792-1884)
appuyée sur la méridienne de Delambre et Méchain
6. nouvelle méridienne de France (1870-1896)
- On assiste au XIXe siècle au développement de nombreux réseaux
géodésiques locaux et à la création d'ellipsoïdes.
Cependant la géodésie reste un concept
local
les réseaux nationaux ne concordent
pas entre eux.
Création en 1886 de l'Association Internationale de
Géodésie :
- objectif établir une meilleure collaboration entre
les différents pays.
C'est également à cette époque que l'on se rend compte officiellement que la Terre
n'est pas exactement un ellipsoïde.
=> Grâce aux mesures de pesanteur ;
- matérialisation de la déviation relative de la
verticale
- définition des surfaces équipotentielles de niveau
perpendiculaires en tout point à la verticale locale.
- Au XXe
siècle
Grâce :
- aux progrès des mesures électromagnétiques;
- à la puissance de calcul de l'informatique ;
=> essor
- de la gravimétrie (mesure de la variation des
irrégularités de la gravité, cf. pesanteur in Wikipédia, dues, entre autre, à
l'inégale répartition des masses à l'intérieur de la Terre) ;
- de l'astrogéodésie ;
- des méthodes spatiales.
Techniques permettant d'affiner notre connaissance de
la forme de la terre :
- le géoïde par Wikipedia et par Universcience TV.
La Terre est vue comme une sphère régulière aplatie
aux deux pôles.
Mais c'est une "surface
topographique" avec des vallées
sous-marines et des montagnes (-11 000 m à +8 000 m).
Cette surface n'est pas
définissable mathématiquement.
On définit, alors, un géoïde de référence :
=> suface
équipotentielle du champ de gravité
terrestre ;
Il coïncide avec le niveau
moyen
des mers.
On lira avec intérêt les pages que lui consacre le site du RnCan mais aussi celui de l'IFREMER.
Le géoïde terrestre est une surface de type
océanique en tout point perpendiculaire à la direction de la
force gravitationnelle.
fig. 2/32 - Le géoïde (cfm21f32.gif)

Sources : webzoumine
fig. 2/33 - Le géoïde (cfm21f33.gif)
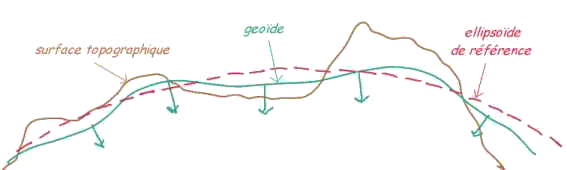
Sources : webzoumine
La géodésie
spatiale :
- a permis d'établir des réseaux qui ceinturent la
Terre pour donner un positionnement absolu et relatif en coordonnées géocentriques.
- est devenue une des bases scientifiques de la
physique du globe pour l'étude des mouvements et déformations de la
croûte terrestre (marées terrestres, tectonique des plaques).
2. Les principaux types de coordonnées
Trois types de coordonnées sont définis dans un système
géodésique :
- les coordonnées
cartésiennes géocentriques ;
- les coordonnées
géographiques sur une surface de
référence ;
- les coordonnées en représentation plane ou projection.
Suivant les techniques utilisées, les coordonnées
obtenues seront différentes.
- en géodésie terrestre => en projection.
- GPS
=> coordonnées
cartésiennes géocentriques.
2.1. Coordonnées cartésiennes géocentrées
fig. 3 - Coordonnées cartésiennes géocentrées
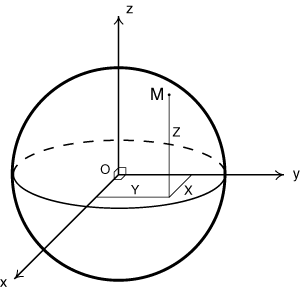
Sources : www.ign.fr
- Comment exprimer les coordonnées
du point M à la surface de la Terre ?
M a les coordonnées
cartésiennes géocentriques suivantes
(X,Y,Z) qui sont prises dans un repère orthonormé :
- dont l'origine est le centre des masses de la
Terre ;
- avec Oz l'axe de rotation de la Terre ;
- Oxy le plan de l'équateur.
- Ces coordonnées sont utilisées :
- en géodésie spatiale ;
- comme intermédiaire lors des calculs de changements
de systèmes géodésiques.
2.2. Surface de référence et coordonnées géographiques
2.2.1. Surface de référence terrestre
- Quelle est la surface de référence
la plus simple mathématiquement et qui représente le mieux possible
les formes de la Terre ?
C'est un ellipsoïde de
révolution => une sphère aplatie aux pôles
fig. 3/34 - L'ellipsoïde de révolution (cfm21f34.gif)
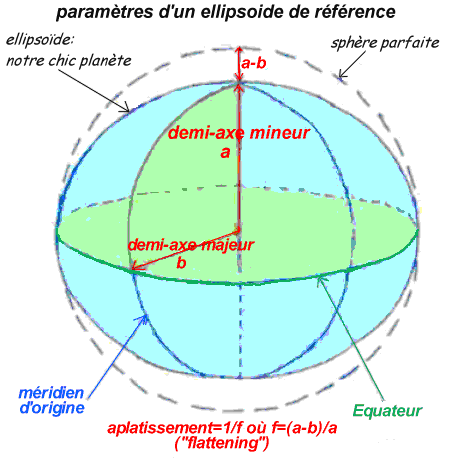
Sources : webzoumine
Il existe de nombreux
ellipsoïdes représentant la Terre.
Leurs dimensions varient de l'ordre de quelques
centaines de mètres.
Le demi-grand axe de l'ellipsoïde a une valeur d'environ
6 370 km et le demi-petit axe une valeur d'environ 6 350 km.
Soit, pour un ballon de football, un aplatissement de
0,3 mm.
2.2.2. Les coordonnées géographiques
fig. 4/15 - Coordonnées géographiques
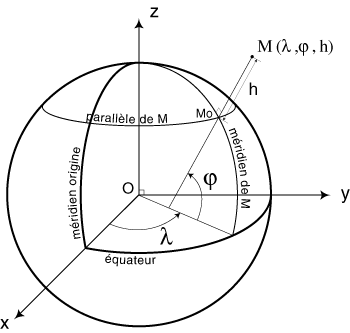
Sources : www.ign.fr
- Comment exprimer les coordonnées
du point M à la surface de la Terre ?
Les coordonnées
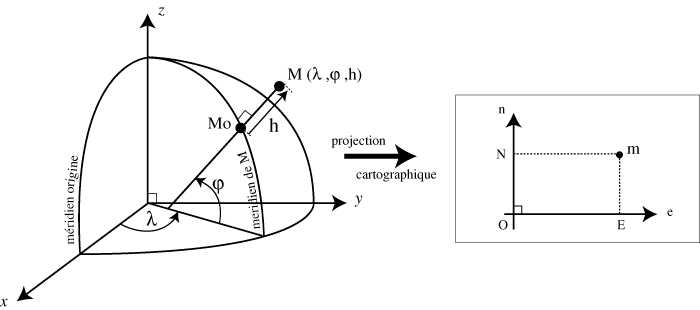
géographiques de M sont la longitude 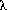 (lambda),
la latitude
(lambda),
la latitude  (phy), projection de M sur l'ellipsoïde suivant la
normale, et h (l'élévation ou hauteur à ne pas confondre avec
l'altitude) est la distance algébrique de Mo à M.
(phy), projection de M sur l'ellipsoïde suivant la
normale, et h (l'élévation ou hauteur à ne pas confondre avec
l'altitude) est la distance algébrique de Mo à M.
Deux façons d'exprimer les coordonnées géographiques
:
- les coordonnées sexagésimales ;
- les coordonnées
décimales.
- Comment passer de l'un à l'autre
?
- pour passer des degrés
sexagésimaux aux degrés décimaux :
DD = D° + M'/60 + S''/3600
- pour passer des degrés
décimaux aux degrés sexagésimaux
:
D° = ENT(DD)
M' = ENT(DD-D°)*60
S'' = (DD-D°-M'/60)*3600
où ENT() est la fonction
"partie" entière (dans Excel par exemple)
La longitude
est un angle orienté entre :
- le plan méridien origine ;
- et le plan méridien contenant le point M.
Le méridien
origine international est celui de
Greenwich (cf. méridien de Greenwich in
: Wikipedia).
- Depuis quand le méridien de
Greenwich est-il le méridien international ?
Il y a autant de méridiens origines que de systèmes
géodésiques (Paris pour la France).
La latitude
est l'angle orienté entre :
- le plan de l'équateur ;
- et la normale à l'ellipsoïde passant par le point M.
La hauteur
est la distance algébrique MoM entre le point M et l'ellipsoïde.
- Quelle est la plus courte
distance entre deux points ?
- sur une sphère, c'est l'orthodromie
(est représentée par une courbe sur une carte !) ;
- sur une carte, un planisphère, c'est la loxodromie (est représentée par une
droite qui coupe les méridiens avec un angle constant, mais n'est pas
la distance la plus courte !).
Voyons ça en pratique : allons de Tokyo à Paris (c'est
par ici) !
Si vous avez envie de faire
quelques calculs de distances sur la sphère, vous pouvez regarder cela !
2.3. Les coordonnées rectangulaires en représentation plane ou
projection
L'utilisation de coordonnées sur une surface de référence
comme un ellipsoïde :
- n'est pas aisée ;
- ne permet pas de réaliser directement
=> des mesures
- de distance ;
- d'angle ;
- de surface.
Il est plus pratique d'avoir une
image graphique du monde sur un plan.
On représente l'ellipsoïde (ou une partie de celui-ci) sur un plan
= une représentation plane ou projection.
fig. 5/16 - Coordonnées en projection
Sources : www.ign.fr
- Comment exprimer les coordonnées
du point M sur un plan ?
M a des coordonnées en
projection. Ce sont les coordonnées cartésiennes (E,N) du point m, image de M dans le plan projection muni
d'un repère orthonormé (O ; e ; n).
La projection cartographique est définie par la
donnée de deux fonctions f et g telles que : E = f (l,i) et N = g
(l,j).
L'objectif de la projection est de
passer des points géographiques d'une surface courbes à une surface
plane.
Mais ceci va entraîner des
déformations.
Selon les propriétés des deux fonctions f et g,
certaines projections vont essayer de conserver tout ou partie des :
- angles ;
- formes ;
- surfaces
- distances.
3. Les projections
Les algorithmes mathématiques permettent de créer des
représentations planes (projections) à l'infini.
Elles sont donc très nombreuses.
En général, on les classe selon ces trois critères :
- type de représentation => qualité géométrique ;
- type de canevas => représentation des méridiens et des parallèles sur le
plan ;
- aspect de la
représentation => orientation de la
surface de projection par rapport à l'ellipsoïde.
3.1. Types de représentation et déformations
3.1.1. Types de représentation
- L'objectif
prioritaire lors de la projection d'une
sphère sur un plan
c'est de limiter les
déformations
En fonction du but à atteindre,
on choisit de conserver localement
:
- les angles => projection
conforme
- conserve localement les angles, donc les formes ;
- mais les surfaces sont
déformées ;
- l'échelle reste la même dans toutes les
directions à partir d'un point.
Objectif
: se localiser, se diriger
- les surfaces => projection
équivalente
- conserve localement les surfaces ;
- plus précisément, ce
sont les rapports de surface qui restent constants ;
- ne conserve pas les angles (le calcul des
distances est, au moins, imprécis)
Objectif
: cartographier à petite échelle en respectant les proportions.
parfois
- ni l'un ni l'autre => projection
aphylactique
- ne conserve ni les angles
ni les surfaces, mais elle peut être "équidistante" lorsqu'elle conserve les distances à partir d'un point donné
(souvent le long d'un méridien).
Mais, aucune projection ne peut conserver toutes les
distances.
- Dans la plupart des projections, le Nord de la projection n'indique pas la direction du pôle Nord géographique.
3.1.2. Les déformations
Chaque projection entraîne des déformations.
Un cartographe français du XIXème siècle est un des
premiers à s'y intéresser : Nicolas-Auguste Tissot
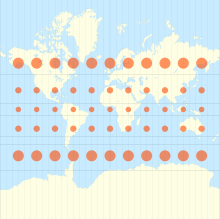
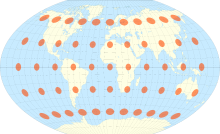
Il met au point un indicateur visuel dit : "Indicatrice
de Tissot".
3.2. Différents types de canevas*
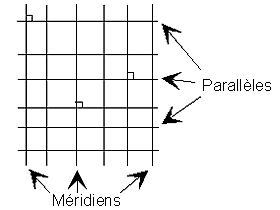
- Canevas simples (!)
|
Canevas cylindrique
|
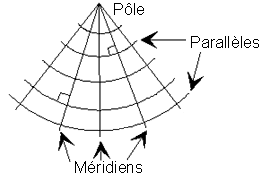
Canevas conique
|
|
fig. 7/22
|
fig. 8/24
|
|
|
|
fig. 9/23
|
fig.10/25
|
|
|
- Canevas moins simples (!!)
|
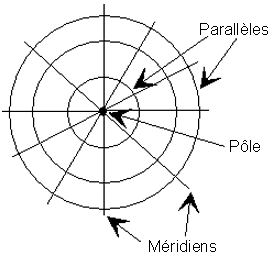
Canevas azimutal
|
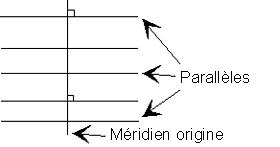
Canevas méricylindrique
|
|
fig. 11/26
|
fig. 12/28
|
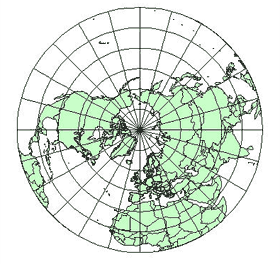
|
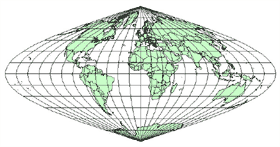
|
|
fig. 13/27
|
fig. 14/29
|
|
|
- Canevas encore plus complexe
|
Canevas mériconique
|
|
fig. 15/30
|
fig. 16/31
|
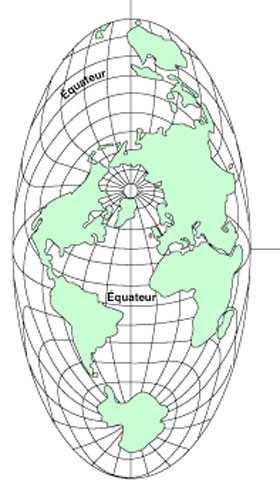
|
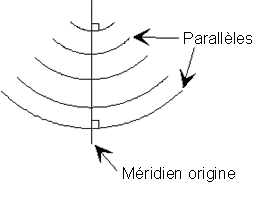
|
Sources : Serge Botton, École Nationale des Sciences Géographiques
www.ign.fr
- Ces figures mettent en évidence la convergence des méridiens :
- c'est l'angle entre le méridien qui passe par un
point et le nord de la projection ;
- cet angle peut atteindre plusieurs degrés (positif ou
négatif).
fig. 6 - Convergence des méridiens
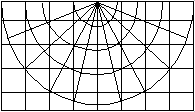
Sources : www.ign.fr
- Dans la plupart des lieux, le pôle Nord magnétique n'est pas dans la direction du pôle Nord géographique.
L'angle entre le Nord magnétique et le Nord
géographique s'appelle la déclinaison magnétique.
3.3. Les (trois) principaux groupes de projections
Ce sont des projections sur des surfaces développables*
A savoir, les projections :
- cylindriques*
- coniques*
- azimutales*
3.3.1. Projections cylindriques
La surface de projection est un cylindre
tangent ou sécant au modèle de la Terre.
- Le plus souvent observée dans sa variété directe*, mais aussi transverse*, plus rarement oblique*.
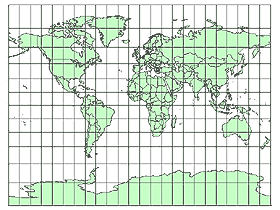
fig. 7 - Représentation cylindrique directe
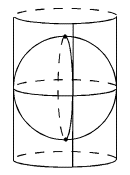
Sources : www.ign.fr
fig. 8 - Représentation cylindrique oblique
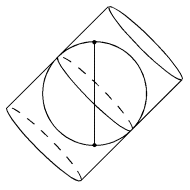
Sources : www.ign.fr
fig. 9 - Représentation cylindrique transverse
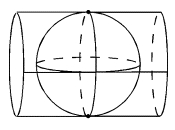
Sources : www.ign.fr
Exemple : UTM, Gauss,...
3.3.2. Projections coniques
La surface de projection est un cône
tangent ou sécant au modèle de la Terre.
Elle est surtout utilisée :
- pour les cartes à grande échelle ;
- dans sa variété directe.
Elle existe sous deux formes :
fig. 12 - Représentation conique directe tangente
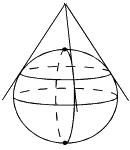
Sources : www.ign.fr
fig. 13 - Représentation conique directe sécante
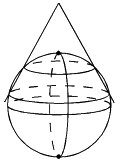
Sources : www.ign.fr
Exemple : Lambert, Lambert-93, Bonne, ...
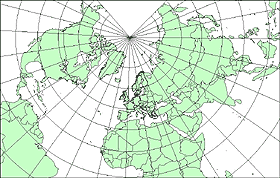
3.3.3. Projections azimutales
Les quatre principaux types de projections azimutales
sont les projections :
- stéréographique ;
- gnomonique
;
- orthographique ;
- projection
azimutale
équivalente de Lambert.
fig. 17 - Quelques représentation de projections azimutales

Sources : Extrait de l'Atlas 2000 (Nathan) in Gilles Davidowicz
4. Quelques prolongements
Il est possible de tester tout cela sur : planet.botany.uwc.ac.za
Dans un hommage à Waldo Tobler, Philippe Rivière
présente sur son blog Visioncarto
des projections
hyperelliptiques dynamiques à l'écran.
Un grand nombre de projections est regroupé et commenté
sur le site de Christian Bordat (actuellement
indisponible). On peut également y télécharger un document
édité par ESRI pour la version 9 d'ArcGis : Comprendre les projections. Document
qui reste d'actualité !
Une vidéo sur la dimension 2 : permet de
mieux comprendre les projections ! Celle-ci, sur Vox (en anglais), est un peu plus nerveuse !
5. Test de compréhension
|
Communiquez-moi sur la plateforme Moodle, à
la rubrique
"Questions de cours",
les réponses aux questions suivantes :
Question n°2.1.1. La
carte topographique de base française (Série bleue) a des
coordonnées imprimées dans ses marges en :
a) Coordonnées cartésiennes géocentrées (x, y,
z)
|
c) Coordonnées rectangulaires en représentation
plane
|
b) Coordonnées géographiques (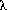 , ,  , h) , h)
|
d) rien de tout cela
|
Question n°2.1.2. La
surface équipotentielle qui coïncide avec le niveau moyen des
mers correspond à la notion de :
a) Surface topographique
|
c) Sphéroïde
|
b) Géoïde
|
d) Ellipsoïde
|
Question n°2.1.3. Quel
siècle faut-il attendre pour démontrer que la Terre est
aplatie aux Pôles ?
a) XVIè
|
c) XVIIIè
|
b) XVIIè
|
d) XIXè
|
Question n°2.1.4. La
carte topographique de base française (Série bleue) est
associée à une projection dite :
a) Conique conforme
|
c) Cylindrique équivalente
|
b) Conique équivalente
|
d) Cylindrique conforme
|
|
Retour au début de la fiche Mémo
Fiche Mémo suivante
NB : les mots suivis de "*" font partie du
vocabulaire géographique, donc leur définition doit être connue.
Faites-vous un glossaire.