V.1.8 - Dernière mise à jour : 10/10/2007
- 1er cas de figure
- Les caractères sont :
- quantitatifs ;
- des entiers ;
- tous positifs ;
- regroupés dans un tableau de contingences*
- Le tableau de contingences est constitué de :
- n individus statistiques ;
qui peuvent être des unités spatiales (tableau de données = tableau d'information géographique)
- p variables quantitatives.
Alors,
- il est possible d'effectuer sur ce tableau une Analyse des correspondances simples, ou binaires.
- 2e cas de figure
- Les caractères sont :
- qualitatifs ;
- des effectifs (fréquences absolues) ;
- tous positifs ;
- regroupés dans un tableau quelconque qui sera transformé en un tableau disjonctif complet* (dans certains cas appelé tableau logique)
- Le tableau disjonctif complet est constitué de :
- n individus statistiques ;
qui peuvent être des unités spatiales (tableau de données = tableau d'information géographique)
- p variables qualitatives.
Où chaque modalité des variables p :
- devient une "colonne" ;
- est codée en présence / absence (1 ou 0).
Alors,
- il est possible d'effectuer sur ce tableau une Analyse des correspondances multiples.
Comme l'ACP, l'AFC a pour but de hiérarchiser l'information contenue dans un tableau de données. Elle va aussi bien s'intéresser à l'étude des colonnes (variables) qu'à l'étude des lignes (individus) du tableau d'information pour confronter les différentes distributions et permettre :
- de découvrir des irrégularités dans ces distributions ;
- d'analyser des interrelations entre les variables ;
- de mettre en évidence des combinaisons plus ou moins systématiques entre les variables ;
En bref, de dégager des structures dans l'espace géographique étudié, qui ne sont pas forcément linéaires.
Cela passe par une simplification de l'information d'origine
L'AFC se pratique sur :
- des tableaux de contingences ;
ou
- des tableaux quelconques transformés en tableaux disjonctifs complets.
Contrairement à l'ACP, les calculs relèvent
de la métrique du
khi deux* (noté ![]() )
)
- Qu'est-ce qu'un tableau de contingence ?
C'est un tableau constitué de nombres entiers où :
- la somme en lignes a un sens !
- la somme en colonnes a un sens !
tab. 1 - Superficie des types de peuplements en Picardie en 1984 (en ha)
Sources : Superficie en bois et forêts en 1984, Statistique agricole annuelle 1984, Ministère de l'Agriculture, SCEES
Feuillus Résineux Mixtes Total par dép. Aisne 106 500 3 380 1 470 111 350 Oise 101 700 10 000 0 111 700 Somme 45 200 4 350 50 49 600 Total Picardie 253 400 17 730 1 520 272 650
Faire une ACP ou une AFC, c'est chercher à établir des degrés :
- de ressemblance ;
et
- de différence entre les unités spatiales (ou les variables).
- Pourquoi ne pas garder la même métrique que dans l'ACP pour les peuplements forestiers de la Picardie ?
Si l'on choisit la distance euclidienne sur les données brutes pour mesurer ces différences entre départements, on obtient les écarts suivants :
d(Aisnes ; Oise)2 = (106 500 - 101 700)2 + (3 380 - 10 000)2 + (1 470 - 0)2 = 69 025 300
d(Aisnes ; Oise) = (69 025 300)1/2 = 8 308,1 ha
d(Aisnes ; Somme) = 61 324,1 ha
d(Oise ; Somme) = 56 781,8 ha
L'Aisnes et l'Oise se ressemblent alors que la Somme diffère.
Pourtant, sur le tableau 1 les profils de l'Oise et de la Somme, avec une forêt mixte très faible, sont très proches.
- Dans ce contexte, la distance euclidienne transcrit les différences de masse entre les départements :
L'Aisnes et l'Oise se ressemblent car leurs superficies sont proches.
- Pour éliminer l'artefact lié aux ordres de grandeur, il faut transformer les données :
en pourcentage, par exemple !
Mais attention, le tableau des pourcentages n'est plus un tableau de contingences.
tab. 2 - Part des types de peuplements en Picardie en 1984 (en %)
Sources : Superficie en bois et forêts en 1984, Statistique agricole annuelle 1984, Ministère de l'Agriculture, SCEES
Feuillus Résineux Mixtes Part du dép. dans la région Aisne 95,6 3,0 1,3 40,8 Oise 91,0 9,0 0,0 41,0 Somme 91,1 8,8 0,1 18,2
Si l'on choisit la distance euclidienne sur les données relatives pour mesurer ces différences entre départements, on obtient les écarts suivants :
d(Aisnes ; Oise)2 = (95,6 - 91,0)2 + (3 - 9)2 + (1,3 - 0)2 = 57,9
d(Aisnes ; Oise) = (57,9)1/2 = 7,6 %
d(Aisnes ; Somme) = 7,4%
d(Oise ; Somme) = 0,2%
Cette fois, l'Oise et la Somme apparaissent bien comme se ressemblant le plus avec leurs forêts mixtes pratiquement nulles.
Pour annuler l'effet de masse, il est également possible de pondérer les distances.
- Qu'est-ce qu'une distance pondérée ?
C'est, par exemple, une distance euclidienne entre les profils (les lignes) des individus ou chaque terme est pondéré par l'inverse du poids relatif de la variable (colonne) correspondante.
Dans les calculs de distance, cette pondération :
- renforce le poids des variables de masse faible ;
donc
- compense les différences de poids entre les variables.
Sa formulation est la suivante :
formule n°1 - (mem03dea.htm)
Avec :
tab. 3 - Notations du tableau de contingence
j = 1 2 . j j' . p Somme en lignes i = 1 k 1 1 k 1 2
k 1 . 2 k 2 1
k 2 . .
i
k i j k i j'
k i . i'
k i' j
k i' . .
n
k n . Somme en colonnes k . 1 k . 2
k . j k . j'
k . .
Si l'on choisit la distance euclidienne pondérée sur les données brutes pour mesurer ces différences entre départements, on obtient les écarts suivants :
Ce fichier est au format Excel (.xls) et "pèse" 193 Ko.
d(Aisnes ; Oise) = (0,0543)1/2 = 0,30
d(Aisnes ; Somme) = 0,39
d(Oise ; Somme) = 0,02
Cette fois encore, l'Oise et la Somme apparaissent bien comme se ressemblant le plus.
Cette distance pondérée s'appelle la métrique* (ou distance) du
, prononcer Khi2*.
tab. 4 - Récapitulatif des distances entre les départements (individus) de Picardie
Dist. euclidienne sur données brutes Dist. euclidienne sur données relatives (%) Distance du d(Aisnes ; Oise) 8 308,1 0,076 0,23 d(Aisnes ; Somme) 61 324,1 0,074 0,22 d(Oise ; Somme) 56 781,8 0,002 0,01
Remarques :
- Il ne faut pas comparer les distances entre elles, mais la hiérarchie à l'intérieure d'une distance ;
- La distance euclidienne sur les données brutes peut ne traduire que des effets de masse ;
- En raison de la symétrie des pondérations que la métrique du
impose au tableau de contingence, cette distance pondérée peut aussi bien s'appliquer aux lignes (individus) qu'aux colonnes (variables).
Si l'on veut répondre à la question :
- Quels sont les traitements sylvicoles les plus proches en Picardie ?
Alors, la formule devient :
formule n°2 - (mem03dea.htm)
- Qu'apporte la distance du Khi2 ?
La distance du ![]() repose sur la comparaison de profils
repose sur la comparaison de profils
=> la masse des individus est relativisée (mais pas annulée comme lors d'une ACP sur des pourcentages) ;
=> le découpage spatial est peu marqué ;
=> la symétrie entre lignes et colonnes est conservée.
Ils sont très proches de ceux d'une ACP.
Cependant,
il existe quelques différences d'interprétation remarquables dues :
- au nuage de point construit sur les profils (des ligne ou des colonnes) ;
- à la métrique du
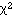
Mais, là encore,
on recherche les droites (les axes factoriels) d'allongement maximum du nuage de point
(celles qui sont les plus proches de tous les points simultanément)
- Chaque axe factoriel est défini par un vecteur dit
vecteur propre*
Les vecteurs propres définissent les différentes directions du nuage d'information
- La part d'information prise par chaque vecteur propre est appelée
valeur propre*
Elle définie la hiérarchie de l'axe factoriel.
- En AFC :
- la 1ère valeur propre est triviale, elle vaut 1 ;
elle ne sert pas à l'interprétation
- toutes les autres sont inférieures à 1 ;
- la plus grande d'entre-elles désigne la variance du 1er axe factoriel ;
- la 2e etc. ;
- la somme de toutes les valeurs propres mesure l'inertie totale du nuage.
- le degré de différenciation introduit par un axe est d'autant plus grand que sa valeur propre est élevée.
- Comme pour l'ACP :
- valeur propre = part de variance (d'information) du nuage prise en compte par l'axe
- elle est généralement exprimée en pourcentage
on parle indifféremment de pourcentages :
- d'inertie
- d'information
- de variance
- Cependant, contrairement à l'ACP :
- on étudie également les valeurs brutes des valeurs propres, car les 2 informations sont complémentaires :
- le taux d'inertie associé à une valeur propre permet l'analyse de la concentration de l'information sur l'axe ;
- la valeur brute permet l'analyse de la dispersion de l'information sur l'axe, donc la mesure de la différentiation spatiale (cas des tableaux d'information géographiques)
- les coordonnées, contributions ou qualités s'interprètent de la même façon
que l'on s'intéresse aux variables ou aux individus.
- indiquent les positions relatives des variables (ou celles des individus) :
- les unes par rapport aux autres ;
et
- par rapport au centre de gravité du nuage.
- contrairement à l'ACP, où ce sont des coefficients de corrélation.
Synonyme = contributions absolues*
- indiquent le rôle relatif des variables (ou celles des individus) :
- dans la formation (la caractérisation) ;
donc
- dans la dispersion ;
de l'axe factoriel
Elles permettent de repérer quelles sont les variables (ou les individus) les plus contributives par axe
- la somme des contributions vaut 1
- généralement exprimée en pourcent ou pour mille
Elles permettent :
- d'identifier les variables (ou les individus) qui définissent le mieux les axes ;
les plus contributives !
- Contrairement à l'ACP, deux variables (ou individus) peuvent être projetés au même endroit sur l'axe :
- avoir les mêmes coordonnées ;
- sans avoir les mêmes contributions.
Car la masse de la variable (ou de l'individus) intervient dans le calcul de la contribution en AFC (cf. métrique du khi2).
Donc, dans l'AFC, l'analyse des contributions revêt plus d'importance que dans l'ACP.
Synonyme = contributions relatives*
- permet de caractériser les variables (ou les individus) par les axes
- mesure la part de l'écartement d'une variable (ou d'un individu) au centre de gravité prise en compte par un axe
QLT = cos2 [de l'angle entre le vecteur-variable (ou individu) et l'axe]
cos2 (0°) = 1
=> variable (ou individu) sur l'axe
=> description parfaite de la variable (ou de l'individu) par l'axe
cos2 (90°) = 0
=> variable (ou individu) perpendiculaire à l'axe
=> description nulle de la variable (ou de l'individu) par l'axe
- généralement exprimée en pourcent ou pour mille
Ils complètent les indicateurs fournis pour chaque axe factoriel.
- La contribution* [ou Inertie relative*, INR(i)] de chaque variable (ou de chaque individu) à la dispersion du nuage de points.
=> s'obtient par le rapport de la distance de chaque variable (ou de chaque individu) au centre de gravité du nuage de points sur l'inertie totale du nuage de points.
formule n°3 - (mem03dea.htm)
Avec, ici dans le cadre du calcul de la contribution d'un individu :
INR(i) => inertie relative d'un individu i ;
fi. => sa fréquence ;
d2(i , G) => sa distance au centre de gravité, G, du nuage de points.
- une faible valeur pour la variable (ou l'individu) indique un profil proche du profil moyen ;
- une forte valeur pour la variable (ou l'individu) indique un profil caractéristique par rapport aux autres.
- La qualité* de représentation par rapport à l'ensemble des n 1er axes factoriels
=> s'obtient par l'addition de la qualité de chacun des n axes
Une faible valeur pour la variable (ou l'individu) indique un caractère marginal sur l'ensemble du nuage.
- La masse relative de chaque variable (ou de chaque individu).
- L'inertie totale*
=> s'obtient par l'addition de toutes les valeurs propres brutes
Lors d'études diachroniques (comparaison de recensements, ...), permet de voir si l'on va vers une homogénisation ou une spécialisation
Remarques :
L'ACP et l'AFC présentent des différences fondamentales, mais :
- bien souvent, c'est la nature des données et les objectifs qui font choisir l'une ou l'autre ;
- parfois, une simple transformation des données permet d'utiliser l'une ou l'autre.
Toutefois,
- si l'ACP ne se pratique que sur des données quantitatives ;
- l'AFC accepte :
- les données quantitatives ;
- les données qualitatives
mais les tableaux doivent être :
- de contingence
ou
- disjonctifs complets.
Exemple n°1 : Tableau 3.1 - La structure
socio-professionnelle des salariés (Pop Act en 1990) dans les
régions françaises (en nb d'emplois), (Sources :
Céline ROZENBLAT "Les salaires dans les régions
françaises." Feuilles de Géographie, II-1994, Feuilles
n°7, 10 p.)
Ce fichier est au format texte tabulé (.txt) et "pèse" 10 Ko.
Exemple n°2 : Tableau 3.2 - Le nombre de voies obtenues par les candidats aux élections présidentielles de 2002 (1er tour et 2e tour), (Sources : Conseil constitutionnel)
Ce fichier est au format texte tabulé (.txt) et "pèse" 15 Ko.
L'objectif de cet exemple est voir comment s'opèrent les regroupement et comment l'ajout de deux variables illustratives complète l'analyse.
Exemple n°3 : Tableau 3.3 - Surface en ha des différents postes d'occupation du sol issus de la base de données Corine Land Cover pour 156 communes de Côte-d'Or.
Ce fichier est au format texte tabulé (.txt) et "pèse" 15 Ko.
Exemple n°4 : Tableau 3.4 - La structure pastorale éthiopienne par awrajas (en nombre de têtes), [Sources : EASTMAN (J.R.) - 1997 - 10. Database Workshop. in : IDRISI for Windows. Tutorial Exercises. Version 2.0. Worcester (MA, USA), Clark University, pp. 69-79 et traduction française GODARD, 2003]
Ce fichier est au format Excel (.xls) et "pèse" 51 Ko.
Ce tableau est le support d'un exercice détaillé sur la fiche guide 1.8 du cours de SIG.
L'import des données se fait comme expliqué sur la fiche mémo mem04dea.htm du cours de Master 2 recherche.
Récapitulatif :
Il n'est pas possible de dire que l'AFC est meilleure que l'ACP, et vice-versa.
On privilégie simplement une certaine forme d'entité de base lorsque l'on prend une méthode plutôt qu'une autre :
- c'est l'agrégat (département, région, ...) qui est privilégié par l'ACP sur les données en %.
- c'est l'individu (salarié, électeur, ...) qui est privilégié par l'AFC sur les données brutes.
Exemple n°5 : AMAT (J.-P.), GODARD (V.), HOTYAT (M.) - 2003 - Milieu, gestion, histoire et scénarios de reconstitution dans les sylvosystèmes touchés par les tempêtes de décembre 1999, GIP-ECOFOR, Min. agriculture, 115 p.
Analyse des dégâts en Forêt d'Armainvilliers
Téléchargement du fichier des données
Ce fichier est au format .xls et "pèse" 97 Ko.
Ce fichier est au format .pdf et "pèse" 4,5 Mo !!.
- Modifier les répertoires par défaut
Menu Option + Paramètres généraux ...
Répertoires utilisés par défaut
pour les bases : D:\geo\Votre_Nom\Armain
pour les modèles : D:\geo\Votre_Nom\Armain
pour les filières : D:\geo\Votre_Nom\Armain
zone temporaire : D:\geo\Votre_Nom\temp
les importations : D:\geo\Votre_Nom\Armain
- Enregistrer la feuille Spad en .txt
=> dfm03ta4.txt
- Importation du fichier texte
- Base / Importer... / Importation fichier Ascii ...
SPAD demande :
- Spad version 5.6
Dans une fenêtre Importation fichier Ascii ...
- Cliquez sur Récupérer
- Sélectionner => dfm03ta4.txt
- Nom de l'importation
dfm03ta4
- La sélectionner pui l'ouvrir
- Spad version 5.5 et antérieure
- de localiser le fichier ".txt"
- le format du fichier
- délimité
- séparateur tabulation
- décimale point
- de cocher si la 1ère ligne contient le libellé des variables
- de cocher "Utiliser les X premiers caractères ..."
Sinon vos libellés seront illisibles !!!
valider en cochant Suivant
- de définir les variables en :
- Type
avec :
C1 => Identificateur (Idr_id) ;
C2 => Continue (surf) ;
C3 à C25 => Nomi. à recoder (ch10 à RES2) ;
C26 à C27 => Continue (altm et altM);
C28 à C31 => Nomi. à recoder.
- Libellé
- facultatif, remplace en 60 caractères maxi le titre dans la base
- Code Id.
- option pour les QCM ;
- pour recoder des variables (nominales ou alphabétiques) de même type.
N'hésitez pas à consulter l'Aide !
- Pourquoi "Nomi. à recoder" ?
Cela signifie que :
0 => 1 1 => 2 2 => 3 3 => 4 Sinon le zéro est une valeur manquante et Spad met toutes les variables en continue !
- Exécuter l'importation
- enregistrement de la base au format ".sba"
=> dfm03ta4.sba
- si l'importation se passe bien, consulter :
- les statistiques de la bases
- l'édition des résultats
- l'édition du compte-rendu qui signale toutes les anomalies lors de l'importation
- codes inattendus,
- variables transformées, ...
- si l'importation comporte des erreurs :
- la base n'est pas générée
- cliquer sur le bouton "Il y a des erreurs" qui édite le compte rendu ;
- corriger (!!!) puis relancer l'exécution.
- Enfin, cliquer sur OK, puis Fermer.
- Ouvrir une filière prédéfinie
Menu Filière + Filière prédéfinie (ou Ctrl + F)
- Sélection d'une filière prédéfinie
- Groupes de filières prédéfinies : Analyses factorielles et classification
- Filières prédéfinies : Analyse des correspondances multiples
- Valider par OK
- Choisir une base
Filière + Sélectionner base
D:\geo\Votre_Nom\Armain\dfm03ta4.sba
- Méthode + Paramètres ... (ou Shift + F6)
Onglet Variables
- Sélection des variables : Nominales actives
=> toutes
- Sélection des variables : Continues illustratives
=> les trois
Onglet Individus
- Choix des individus
=> tous
Onglet Pondération
=> Uniforme
Onglet Paramètres
- Paramètres de fonctionnement :
Coordonnées conservées les 10 premières
Ventilation 2%
- Paramètres d'édition :
Tableau de Burt Non
Coordonnées éditées les 10 premières
Résultats pour les individus Non
- Fichier pour application tableur : Oui
Options pour application tableur : Non
- Valider par OK deux fois
- Méthode + Exécuter méthode (ou Shift + F5)
- Méthode + Paramètres ... (ou Shift + F6)
Onglet Commande de description
- Liste des axes à décrire : 1-10
- Avec les éléments :
Modalités Actives seules
Variables continues Illustratives seules
Individus Actifs seuls
Onglet Paramètres
Laisser Défaut
- Méthode + Exécuter méthode (ou Shift + F5)
- Méthode + Paramètres ... (ou Shift + F6)
Onglet Paramètres
- Choix de la méthode : Hiérarchique (RECIP)
La méthode SEMIS est une méthode mixte pour classer les très grands nombres d'individus.
- Paramètres de fonctionnement :
Coordonnées utilisées pour l'agrégation : 10 premières
Sauvegarde partielle de l'arbre (nombre d'éléments terminaux) : 50
- Paramètres d'édition :
Histogramme des indices : 50
Composition des éléments terminaux : Non
Coordonnées des éléments terminaux : 10 premières
Caractéristiques des noeuds : Oui
Dendrogramme (arbre hiérarchique) : Large
- Méthode + Exécuter méthode (ou Shift + F5)
- Méthode + Paramètres ... (ou Shift + F6)
Onglet Choix des partitions
- Recherche automatique des meilleurs partitions :
Nombre de partitions : 3
Nombre minimum de classes par partition : 3
Nombre minimum de classes par partition : 10
Onglet Paramètres de partitionnement
- Paramètres de partitionnement :
Itérations de consolidation : 10
Affectation des individus illustratifs aux classes les plus proches : Oui
- Paramètres d'édition :
Correspondance classes-individus Pour tous les individus
Cochez pour Type d'édition
Composition de chaque classe
Classe d'appartenance des individus
Coordonnées éditées pour les classes Les 5 premières
Édition des parangons Nombre 10
- Fichier pour application tableur : Oui
Onglet Caractérisation des partitions
=> par défaut
- Méthode + Exécuter méthode (ou Shift + F5)
- Enregistrement et exécution de la filière
- Filière + Enregistrer filière sous ...
D:\geo\Votre_Nom\Armain\dfm03ta4.fil
Donner un titre "causant", car il apparaîtra sur le bandeau de la fenêtre
- Filière + Exécuter filière (ou F5)
Après avoir
- vectorisé dans CartaLinx les limites des parcelles d'Armainviliers ;
- importé le fichier vecteur dans Idrisi ;
Il faut importer le résultat des classifications de Spad dans Idrisi.
Prendre l'onglet Parti10 du fichier résultat Excel
Il contient
en colonne B => les identifiants
en colonne C => les n° de classes
- Éliminez la colonne A
- Remplacez les en-têtes par :
en colonne B => Idr_id
en colonne C => Classes
- Enregistrez cet onglet en .dbf dans le répertoire qui contient le fichier vecteur
Fichier\Enregistrer sous
Type de fichier DBF 4 (dbaseIV)
arma10cl.dbf
Ouvrir le Database Worshop
File\Import xBase (dbf)
Name of DBF file to be imported => arma10cl.dbf
OK
Création du lien entre le fichier vecteur "PARCDEGA" (parcelle et dégâts !) et la base de données "ARMA10CL"
- Exécuter l'éditeur de collection Collection Editor
File menu / Collection Editor
ou à l'aide de l'icône ci-dessous,
- Ouvrir depuis son menu Fichier
File menu / New ...
- Sélectionner les fichiers liés de type vecteurs (*.vlx)
Files of Type => Vector link files (*.vlx)
- Lui donner le nom PARCDEGA.VLX
- Remplir les 4 composants :
- le nom de la couche vecteur [Vector spatial frame file (vct)] => PARCDEGA
Elle décrit des objets avec un identifiant entier unique.
- le nom du fichier base de données [Database file (mdb)] => ARMA10CL
C'est un fichier au format Microsoft Access. Les formats dBASE (.dbf) sont convertis par le Database Workshop.
- le nom de la table [Table] => ARMA10CL
Une base de données peut contenir de très nombreuses tables.
Le fichier VLX indique quelle table utiliser (ici, il n'y a que celle là !).
- le nom du champ clef [Link field] => IDR_ID
Il établit le lien entre la base de données et les objets vecteurs.
- Sauvegarder puis fermer l'éditeur de collections.
- Rouvrir la base de données ARMA10CL à partir du Database Workshop
La typologie peut être cartographiée comme vue sur la fiche guide 1.8, soit depuis le Database Worshop, soit comme couche raster. Il peut être intéressant de transférer les classes du champ de la base de données, où il est stocké, à un fichier raster où il sera plus manipulable. Trois étapes sont nécessaires. C'est d'abord un export depuis le Database workshop, puis la création d'un fichier raster vide avec le module INITIAL et enfin l'intégration dans ce raster vide avec le module ASSIGN qui vont le permettre.
- Réaliser l'exportation depuis le Database workshop.
Dans la fenêtre du gestionnaire d'exportation (Value File Manager)
- Nom du fichier attributs (Value file name) => ARMA10CL
- Nom du champ lien (Link field name) => Idr_id
- Nom du champ à compléter (Data field name) => CLASSE
- Valider par OK.
ae) Création du fichier raster vide depuis le menu :
- Laisser cocher la définition spatiale des paramètres sur une autre image (Copy spatial parameters from another image) ;
- Fichier sortie à créer (Output image) => ARMA10CL
- Copier les paramètres spatiaux de l'image suivante (Image to copy parameters from) => DEGATS ;
- Type des données de sortie (Output data type) => Réels (Real)
- Laisser la valeur initial par défaut => 0
- Valider par OK.
af) Remplissage du fichier raster vide depuis le menu :
- Laisser cocher le type de fichier par défaut (File type) => Raster file
- Image contenant les objets spatiaux (Feature definition image) => PARCDEGA
C'est une image raster et non un fichier vecteur qui est demandée ici. Elle doit contenir le numéro des objets spatiaux pour accueillir les attributs du fichiers valeurs (.AVL). Si elle n'existait pas, il faudrait la créer avec le module POLYRAS à partir du fichier vecteur qui contient les identifiants des parcelles.
- Fichier sortie à compléter (Output image) => ARMA10CL
- Fichier attribut (Attribut value file) => ARMA10CL
- Titre du fichier de sortie (Output title) => Typologie des dégâts en forêt d'Armainvilliers
- Valider par OK.
puis
- Accepter d'écraser le fichier existant.
Il est vide, il ne contient que des zéros !
La carte apparaît !
- Valider par OK.
Attention, là encore, si le fichier attributs ARMA10CL.AVL contient des "," et pas des ".", vous riquez d'avoir le message d'erreur suivant "Check right hand column of values file for blanks or non-numeric values" !!!
Convertissez les "," en "." dans le fichier ARMA10CL.AVL dans Edit par le menu Tools / Find and Replace ...
NB : les mots suivis de "*" font partie du vocabulaire statistique, donc leur définition doit être connue. Faites-vous un glossaire.