- sa moyenne*
formule n°1 - fm31
- sa variance*
formule n°2 - fm31
- ou son écart-type* dans l'univers* "u"
formule n°3 - fm31
Univers et population sont synonymes
V.1.4 - Dernière mise à jour : 21/11/2008
Lorsque l'on étudie un caractère quelconque :
- pourcentage de boisements sur une photo ou une carte ;
- surface enherbée sur un territoire communale ...
sur une population d'effectif* M
On peut le résumer par :
- sa moyenne*
formule n°1 - fm31
- sa variance*
formule n°2 - fm31
- ou son écart-type* dans l'univers* "u"
formule n°3 - fm31
Univers et population sont synonymes
Un caractère qualitatif codé en présence ou absence
Il a pour moyenne une proportion :
formule n°4 - fm31
et pour variance :
formule n°5 - fm31
toujours calculés sur la population
Cependant, lorsque la population est importante
- on n'a matériellement pas le temps d'interroger toutes les unités statistiques
- on va procéder par échantillonnage
Or si l'on n'est pas exhaustif*,
ces paramètres ne seront jamais connus exactement !
Existe-t-il une solution ?
- Si l'on tire un échantillon équiprobable avec remise d'effectif m parmi la population M
Traduction :
- équiprobable : chaque individu a une chance identique d'en faire partie
- avec remise : une fois tiré et le caractère "y" observé, on le remet (il peut donc être, en théorie, tiré une seconde fois)
On est dans le cas des sondages aléatoires simples*
Synonyme : sondages élémentaires*
- On peut calculer sur cet échantillon :
- sa moyenne
qui est un estimateur sans biais de
la moyenne (inconnue) sur la population
- son écart-type "s"
- Cette moyenne ![]() dépend de
l'échantillon tiré
dépend de
l'échantillon tiré
- Si on recommence plusieurs fois le tirage
on aura différentes valeurs de
C'est une variable aléatoire*
- Quand :
- m est assez grand (en pratique > 30)
et que
- n (le nombre d'échantillons) tend vers l'infini
La distribution de toutes les valeurs des moyennes
![]() fournies par tous les échantillons que le hasard
désigne, à la forme d'une courbe en cloche (cf. fig.
1).
fournies par tous les échantillons que le hasard
désigne, à la forme d'une courbe en cloche (cf. fig.
1).
fig. 1 - Distribution des moyennes d'échantillon
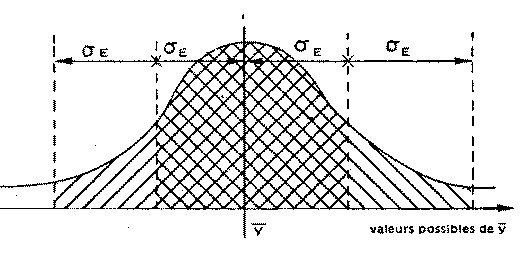
- La moyenne des échantillons ![]() suit une loi
normale* quelle que soit la
distribution de la variable sur l'univers
:
suit une loi
normale* quelle que soit la
distribution de la variable sur l'univers
:
- centrée sur
(la moyenne sur l'univers) , appelée Espérance mathématique* et notée E(
) ;
- de variance
formule n°6 - fm31
ou
- d'écart-type
formule n°7 - fm31
appelé erreur-type*
C'est le théorème central limite*
- On peut estimer ![]() (le caractère inconnu mais recherché, ici
la moyenne sur l'univers)
(le caractère inconnu mais recherché, ici
la moyenne sur l'univers)
- à l'intérieur d'une fourchette d'estimation appelée intervalle de confiance*
- moyennant une prise de risque liée à l'échantillonnage
- Cette estimation se présente comme suit :
D'après l'échantillon, on estime que
![]() appartient à l'intervalle
de confiance
appartient à l'intervalle
de confiance
formule n°8 - fm31
avec un certain risque d'erreur
où :
t, le t de Student représente un coefficient fonction :
- du risque d'erreur admis ;
- du nombre de degrés de liberté* (cf. Annexe n°1 ).
- 9 chances sur 10 pour que
soit compris dans l'intervalle
formule n°9 - fm31
- 95 chances sur 100 pour que
soit compris dans l'intervalle
formule n°10 - fm31
D'où viennent les coefficients 1,645 et 1,96 ?
- Ils sont lus dans la table de "t"
Où :
- le nombre de degrés de liberté (d.d.l.) renseigne sur le nombre de valeurs libres
[le nombre d'informations libres, non fixées (cf. Annexe n°1 )]
- la probabilité
est le risque d'erreur que l'on se fixe pour déterminer la taille de l'intervalle de confiance
Par exemple, si :
formule n°11 - fm31
alors, on admet que dans 5 échantillons sur 100 que l'on pourrait constituer,
n'est pas compris dans l'intervalle
formule n°10 - fm31
mais
est compris dans cet intervalle dans les 95 autres pour 100 des cas !
- Cependant, ![]() est inconnu, mais
est inconnu, mais
-
formule n°6 - fm31
donc
-
formule n°7 - fm31
et
-
est estimé sans biais par s2
formule n°12 - fm31
variance de l'estimateur
calculée sur l'échantillon
- Exemple (toute ressemblance ...) :
1) Estimation d'un trajet dans un parc d'après le dessin des enquêtés
- Quelle est la distance moyenne parcourue par les promeneurs qui ont fréquenté le parc de La Courneuve entre le 27 octobre et le vendredi 9 novembre 2007 ?
On en a enquêté 75 pendant cette période sur un total théorique de 76 000 (source enquête SERDA 2006 p.3, Téléchargement du document)
Calculer l'intervalle de confiance à l'aide de l'échantillon (Téléchargement du fichier Excel) qui va permettre d'estimer la distance moyenne parcourue par l'ensemble des promeneurs du parc sur cette période
2) Estimation téorique
- Quelle est la distance moyenne parcourue par les habitants de la ville de Trifouillis (20 000 hab.) pendant le week-end de la Toussaint pour acheter des chrysanthèmes et se rendre au cimetière ?
On en sonde 900 d'entre eux :
- la distance moyenne est de 120 km ;
- la variabilité, connue par l'écart type (s) est de 5 km.
On n'a donc pas besoin de calculer :
formule n°12 - fm31
Au risque de se tromper dans seulement 5 % des cas ( ![]() = 0,05)
et pour un tirage avec remise :
= 0,05)
et pour un tirage avec remise :
- 2 *
<
<
+ 2 *
120 - 2 *
<
< 120 + 2 *
120 - 2 * (5 / 30) <
< 120 + 2 * (5 / 30)
120 - 2 * 0,1667 <
< 120 + 2 * 0,1667
119,6666 <
< 120,3334
- La distance moyenne parcourue par les Trifouillois est comprise entre 119,67 km et 120,33 km au risque de 5 %.
ou encore
- La distance moyenne parcourue par les Trifouillois est de 120 km ± 0,33 km au risque de 5 %.
- Remarque :
La précision de l'estimation ne dépend pas :
- du taux de sondage "f"
formule n°13 - fm31
- ni de M, la taille de l'univers
mais de la racine carré de "m" la taille de l'échantillon,
formule n°7 - fm31
Donc il faut raisonner en nombre d'unités enquêtées et pas en taux de sondage
Le coefficient de
variation* "CV" donne une idée de
la précision
relative* de l'estimation de ![]()
formule n°14 - fm31
C'est un indicateur de la concentration* de la distribution autour de

- Exemple (suite) :
- Quelle est la variabilité de l'estimation de la distance moyenne parcourue par les habitants de la ville de Trifouillis ?
Toujours avec un tirage avec remise au risque de 5 %, on prend :
formule n°14 - fm31
- Soit
CV = (0,1667 / 120) = 0,00139
- La variabilité de cette estimation est de 0,14 % au risque de 5 %.
En résumé :
- l'estimateur
est centré sur la valeur recherchée
;
- sa distribution est d'autant plus concentrée autour de
que:
- la taille de l'échantillon m est grande ;
- la variable est peu dispersée dans l'univers.
- le sondage aléatoire permet d'estimer la précision de l'estimation (erreur aléatoire)
|
Communiquez-moi par courrier électronique les réponses aux questions suivantes Question n°3.1.1. La variance renseigne sur :
Question n°3.1.2. Multiplier par 4 le nombre d'individus dans l'échantillon, c'est réduire l'intervalle de confiance d'un facteur :
|
NB : les mots suivis de "*" font partie du vocabulaire statistique, donc leur définition doit être connue. Faites-vous un glossaire.