, prononcer
Khi2*, est
dû à Karl Pearson (Mathématicien anglais, 1857 -
1936)
V.2.31 - Dernière mise à jour : 07/01/2010
Comment étudier 2 à 2 des variables qualitatives ?
- cas des variables à 2 modalités
- cas des variables à plus de 2 modalités
Dichotomiques = deux modalités
Pour passer du tableau de collecte à celui de contingence*
- Qui réussit le mieux au Bac ?
Exemple du chef d'établissement :
- Pour chaque élève, il connaît son sexe et son résultat
tab. 1 - Tableau élémentaire
Identificateur de l'élève Sexe Résultats
1 = masculin + = réussite
2 = féminin - = échec 1 1 + 2 2 + 3 2 - 4 2 + ... ... ... 200 1 - V1 - le sexe => variable nominale dichotomique (2 modalités) repérée et explicative
V2 - les résultats => variable nominale dichotomique (2 modalités) repérée et à expliquer
- Résultats sont reportés dans un tableau dit tableau de contingence* (croisé* ou à double entrée)
tab. 2 - Tableau de contingence
Réussite Échec Total Lignes Garçon 30 40 70 Fille 90 40 130 Total Colonnes 120 80 200
- La distribution marginale* correspond au tri à plat de la variable
On voit en :
- Total lignes => + de filles que de garçons à se présenter
- Total Colonnes => + de réussite que d'échecs dans cet établissement
- dans les cases => 30 garçons qui réussissent, etc...
- Mais, qui réussit le mieux ?
Construction des résultats
2 calculs de pourcentages sont possibles :
en lignes et en colonnes
- Que ce passe-t-il si le nombre de garçons et de filles devient identique ?
égal à 100 par exemple
tab. 3 - Pourcentages en lignes
Réussite Échec Total Lignes Garçon 30 / 70 = 43% 40 / 70 = 57% 70 / 70 = 100% Fille 90 / 130 = 69% 40 / 130 = 31% 130 / 130 = 100% Total Colonnes 120 / 200 = 60% 80 / 200 = 40%
- Donc
- les filles réussissent mieux au Bac (69%) que le garçons (43%)
- le taux d'échec des garçons (57%) est supérieur à celui des filles (31%)
s'il y avait indépendance, les résultats seraient identiques
- le taux de réussite est supérieur au taux d'échec
- Que ce passe-t-il si le nombre de réussites et d'échecs devient identique ?
égal à 100 par exemple
tab. 4 - Pourcentages en colonnes
Réussite Échec Total Lignes Garçon 30 / 120 = 25% 40 / 80 = 50% 70 / 200 = 35% Fille 90 / 120 = 75% 40 / 80 = 50% 130 / 200 = 65% Total Colonnes 120 / 120 = 100% 80 / 80 = 100%
- Donc
Les garçons qui représentent 35% de l'effectif contribuent pour :
- 25% des réussites
- 50% des échecs
Or, ils étaient supérieurs pour le calcul en lignes !!!
- La méthode des pourcentages ne permet de raisonner que sur l'axe des 100%
pas les 2 en même temps
- Mais elle permet de décrire les relations
Il existe une manière de raisonner sur les lignes et les colonnes
Il faut comparer les résultats observés à ceux obtenus en cas d'indépendance (calculés ou théoriques)
- Calcul de l'effectif théorique d'une case
(Total Ligne * Total Colonne) / Nb total d'unités stat = Effectif si indépendance entre sexe et résultats
en respectant disparité du nombre de filles et de garçons
tab. 5 - Effectifs théoriques
Réussite Échec Total Lignes Garçon (70 * 120) / 200 = 42 (70*80) / 200 = 28 70 Fille (130 * 120) / 200 = 78 (130 * 80) / 200 = 52 130 Total Colonnes 120 80 200
NB : On peut en calculer 1 cellule et en déduire les 3 autres.
42 - 120 = 78 réussites des filles
70 - 42 = 28 échecs des garçons
- Peut-on mesurer l'écart entre l'effectif calculé (théorique) et l'observé ?
tab. 6 - Écarts bruts à l'indépendance
Réussite Échec Total Lignes Garçon 30 - 42 = -12 40 - 28 = +12 0 Fille 90 - 78 = +12 40 - 52 = -12 0 Total Colonnes 0 0
- Résultat positif = sur-représentation
il y a plus d'élèves dans cette case que l'indépendance ne le laissait penser
- Résultat négatif = sous-représentation
il y a moins d'élèves dans cette case que l'indépendance ne le laissait penser
- Mais, les écarts bruts sont à relativiser avec les effectifs théoriques attendus
Car, l'écart brut de +12 est le même dans 1 case à 78 individus et une à 28.
- Calcul de l'écart pondéré d'une case
(Effectif observé - Effectif calculé) / Effectif calculé
tab. 7 - Écarts pondérés à l'indépendance
Réussite Échec Garçon (30 - 42) / 42 = -0,29 (40 - 28) / 28 = +0,43 Fille (90 - 78) / 78 = +0,15 (40 - 52) / 52 = -0,23 L'écart le plus important => échec relatif des garçons
C'est cette case qui :
- contribue le plus à l'écart global
- apporte le plus d'information sur le lien entre les 2 variables
Remarque : si l'effectif théorique est faible, la pondération est à prendre avec circonspection
Pour tester la significativité des résultats
Il peut être utile d'aller plus loin que la sur ou la sous représentation case par case
Il peut être nécessaire d'obtenir 1 indice globale du lien
surtout pour comparer des résultats
L'indice du , prononcer
Khi2*, est
dû à Karl Pearson (Mathématicien anglais, 1857 -
1936)
formule n°1 - (mem51enq.htm)
Avec :
oi valeur de la case observée ;
ci valeur de la case calculée ;
j étant égale à 4 pour 2 variables dichotomiques.
Pour l'ensemble des 4 cases
Si
Si
- Le degré de
signification est lu dans la table du
(cf.
Table
n°1)
pour 1 degré de liberté (ddl).
- le n'est significatif que si les effectifs
calculés sont >
ou = 5 dans chaque case
- Les résultats des filles et des garçons sont-ils identiques ?
- Les différences sont-elles dues au hasard ?
On formule le test de significativité suivant (cf. Annexe 2), où l'hypothèse nulle* est :
H0 : il y a indépendance entre les résultats des filles et des garçons (les différences sont dues au hasard)
= (30-42)2/42 + (40-28)2/28 +
(90-78)2/78
+ (40-52)2/52 = 3,43 + 5,14 + 1,85 + 2,77 = 13,19
Donc rejet de l'Hypothèse nulle,
la différence est significative au seuil de 5%
Si on est une fille ou un garçon, on n'a pas la même "chance" d'être reçu au bac !
- Pour plus de précision,
on recherche dans la table de l'écart-réduit
(cf. Table n°4) au risque correspondant à la
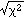
Uniquement pour les tableaux à 4 cases
où on a 2 caractères nominaux dichotomiques
Exemple du bac (suite) :
3,29 <
Donc la différence est significative au seuil de 1 p.1 000
tab. 8 - Table de contingence : l'urbanisation à Volx
Années \ Urbanisation Bâti Non Bâti Total 1960 98 1182 1280 théorique 124,16 1155,84
1990 96 624 720 théorique 69,84 650,16
Total 194 1806 2000
= (98-124,16)2/ 124,16 + (1182-1155,84)2/ 1155,84 + (96-69,84)2/ 69,84 + (624-650,16)2/ 650,16 = 16,888
La différence est significative au seuil de 1 p.1 000
- Mais pour plus de précision, on lit dans la table de l'écart-réduit :
si 3,89 <
alors 0,000 1 <
< 0,000 01
Donc la différence est significative au seuil de 1 p.10 000
Dans le cas de petits échantillons
- lorsque p ou q < 5
- mais supérieurs à 1
[sinon agréger ou recourir aux tables (2A ou 2B, et p.96 de SCHWARTZ 1991)]
formule n°2 - (mem51enq.htm)
- C'est une solution approchée
on diminue la valeur absolue de l'écart de 1/2
- Si on n'applique pas cette correction
on risque de conclure à tort à une signification
- La correction est valable quelque soit la taille de l'échantillon
mais que sur des variables dichotomiques
elle n'est appréciable que si l'échantillon est faible
Si les variables ne sont pas indépendantes
Cas :
- de la double correction
ce n'est pas la correction de 2 échantillons de copies d'un même examen
- d'une succession de traitements (culturaux, médicaux)
c'est le même individu à deux époques successives
Alors, ils faut utiliser une formule de
l'écart-réduit ou un
modifié
Exemple :
- Les 2 photo-interprètes notent-ils pareils ?
Quand corrélation ne signifie pas concordance !
100 points de contrôle ont été inventoriés tour à tour par 2 photo-interprètes
On a donc 100 couples de notes dont on relève juste si elles concordent
tab. 9 - Résultats d'un double contrôle
Par exemple :
Résultats avec les photo-interprètes Nombre de points A B
- - 35 - + 5 + - 15 + + 45
Total 100 - => Non bâti
+ => Bâti
On laisse de côté les 35 "--" et les 45 "++" qui n'apportent rien à la question.
On compare les réponses divergentes (- + et + -)
- Méthode adaptée de l'écart-réduit
formule n°3 - (mem51enq.htm)
où
a = - +
et
b = + -
Si |
Si |
- Le degré de signification est lu dans la
table
de l'écart-réduit .
- La méthode n'est applicable que si :
- (a + b) / 2 > ou = 5
- le nombre de paires considérée dépasse 10
Exemple :
= |15 - 5 | /
(15+ 5)(1/2)
= 10 / (20)(1/2) = 2,24
Les différences de correction sont significatives avec 1 risque inférieur à 3%
- Il est également possible d'utiliser le
à un degré de
liberté
formule n°4 - (mem51enq.htm)
Qui est simplement le carré de l'écart-réduit
- Dans le cas de petits échantillons sur des séries appariées
Les corrections sont les suivantes :
- pour l'écart réduit
formule n°5 - (mem51enq.htm)
- pour le
formule n°6 - (mem51enq.htm)
Conditions d'application :
- Méthode recommandée
quand les effectifs théoriques sont proches de 5
- Méthode insuffisante
quand les effectifs théoriques sont proches de 1 ou 2
Recourir aux tables (tables 2A et 2B SCHWARTZ 1991 pp 282-283)
Dans les séries appariées, il faut :
- tester la différence
mais aussi
- le degré de concordance des réponses
Ce qu'on verra au prochain chapitre (cf. 2.2.3. Notion de concordance)
Pour tester l'intensité de la liaison entre les deux variables
- Lorsque la liaison est significative
On teste l'intensité de la relation entre les deux caractères
- Un grand nombre de coefficients existe :
YULE, KENDALL, de contingence, etc.
- Ces coefficients varient de :
0 => indépendance entre les deux caractères
à
1 => liaison mathématique entre les deux caractères
Ce sont des nombres sans dimension.
- Le coefficient de
Tschuprow*, qui utilise le calculé, est commode
:
formule n°7 - (mem51enq.htm)
avec :
V =>
m => effectif total de l'échantillon de l'échantillon (ma + mb) ;
l => le nombre de modalités du caractère "en lignes" ;
c => le nombre de modalités du caractère "en colonnes" ;
Ce qui renvoie au nombre de degrés de liberté (d.d.1.)
d.d.l. = (l -1) * (c - 1)
Exemple :
- de Volx :
Reprise des résultats calculés sur le tableau 8
T = {16,888 / 2000 * [(2 - 1) * (2 - 1)]^(1/2)}^(1/2) = 0,09
L'indépendance est rejetée mais la liaison n'est pas significative pour autant.
On n'a pas :
- le désert en 1960 ;
- la ville en 1990 !
- du bac :
Reprise des résultats calculés sur l'exemple du bac
T = {13,19 / 200 * [(2 - 1) * (2 - 1)]^(1/2)}^(1/2) = 0,26
Là aussi, l'indépendance est rejetée mais la liaison n'est que faiblement significative.
Le sexe n'explique pas tout !
Analyse très proche des variables qualitatives à 2 modalités
Exemple : tiré de Homo Academicus, BOURDIEU, 1984, éd. de Minuit
- Y a t-il une relation entre la discipline choisie par les enseignants du supérieur et le lycée où ils ont effectué leurs études secondaires ?
Les 2 variables sont repérées
tab. 10 - Discipline et origine des enseignants du supérieur
a) Tableau de contingence
sciences lettres droit médecine total lignes grand lycée parisien 29 47 9 8 93 autre lycée parisien 35 27 11 29 102 lycée de province 51 36 46 17 150 enseignement privé 8 9 20 11 48 total colonnes 123 119 86 65 393 b) Pourcentage en lignes
sciences lettres droit médecine total lignes grand lycée parisien 31,2% 50,5% 9,7% 8,6% 100% autre lycée parisien 34,3% 26,5% 10,8% 28,4% 100% lycée de province 34,0% 24,0% 30,7% 11,3% 100% enseignement privé 16,7% 18,7% 41,7% 22,9% 100% total lignes 31,3% 30,3% 21,9% 16,5% 100% c) Pourcentage en colonnes
sciences lettres droit médecine total lignes grand lycée parisien 23,6% 39,5% 10,5% 12,3% 23,7% autre lycée parisien 28,4% 22,7% 12,8% 44,6% 25,9% lycée de province 41,5% 30,2% 53,5% 26,2% 38,2% enseignement privé 6,5% 7,6% 23,2% 16,9% 12,2% total lignes 100% 100% 100% 100% 100% d) Effectifs théoriques
sciences lettres droit médecine total lignes grand lycée parisien 29,1 28,2 20,4 15,3 93 autre lycée parisien 31,9 30,9 22,3 16,9 102 lycée de province 47,0 45,4 32,8 24,8 150 enseignement privé 15,0 14,5 10,5 8,0 48 total lignes 123 119 86 65 393 e) Écarts pondérés
sciences lettres droit médecine
grand lycée parisien 0,003 0,670 -0,560 -0,480
autre lycée parisien 0,100 -0,130 -0,510 0,720
lycée de province 0,090 -0,210 0,400 -0,310
enseignement privé -0,470 -0,380 0,900 0,390
- Quelles sont les cases qui contribuent le plus à ce lien global ?
Les 3 plus importantes sont positives = surreprésentation :
- enseignement privé et droit + 0,9
- autre lycée parisien et médecine + 0,72
- grand lycée parisien et lettres + 0,67
Il faut toutefois s'assurer de la dépendance entre discipline et établissement secondaire fréquenté.
- Indice et dépendance globale
On calcule le :
pour l'ensemble des cases
Puis on recherche le risque correspondant
nombre de degrés de liberté (d.d.1.)
d.d.l. = (l -1) * (c - 1)
Si >
5% la
différence n'est pas significative au seuil de 5%
Si < ou =
5% la
différence est significative au seuil de
5%
et
- Le degré de
signification est lu dans la table du
(cf.
Table
n°1)
- n'est significatif que si les effectifs calculés
sont > ou
= 5
Exemple BOURDIEU :
= [(29 - 29,1)2/29,1] + [(47 -
28,2)2/28,2]
+ ... + [(20 - 10,5)2/10,5] + [(11 - 8)2/8] = 62,93
avec d.d.l. = (4 -1) * (4 - 1) = 9
< 1 p.1 000 la
différence est hautement significative
Donc il y avait liaison entre discipline et établissement secondaire fréquenté
Mais il faut préciser :
par rapport aux disciplines considérées et aux établissements considérés
Tout autre regroupement ou découpage peut donner 1 autre résultat
Semblable à l'étude de variables nominales
Exemple : Les risques d'avalanche
Comparaison jour à jour du risque avalancheux pour 2 stations de ski sur environ 4 ans
- Y a t-il une différence entre les avis de risques avalancheux de la station A et de la station B ?
tab. 11 - Risque avalancheux pour 2 stations de ski
a) Tableau de contingence
Station A
faible moyen fort total lignes Station B faible 20 100 30 150 moyen 200 20 30 250 fort 10 10 80 100 total colonnes 230 130 140 500 b) Pourcentage en lignes
Station A
faible moyen fort total lignes Station B faible 13% 67% 20% 100% moyen 80% 8% 12% 100% fort 10% 10% 80% 100% total colonnes 46% 26% 28% 100% c) Pourcentage en colonnes
Station A
faible moyen fort total lignes Station B faible 9% 77% 21% 30% moyen 87% 15% 21% 50% fort 4% 8% 57% 20% total colonnes 100% 100% 100% 100% d) Effectifs théoriques
Station A
faible moyen fort total lignes Station B faible 69 39 42 150 moyen 115 65 70 250 fort 46 26 28 100 total colonnes 230 130 140 500 e) Écarts pondérés
Station A
faible moyen fort
Station B faible -0,7 +1,6 -0,3
moyen +0,7 -0,7 -0,6
fort -0,8 -0,6 +1,9
- Quelles sont les cases qui contribuent le plus à ce lien global ?
Les 2 plus importantes sont positives = surreprésentation :
- Risque fort pour les stations A et B + 1,9
- Risque faible pour B et fort pour A + 1,6
bien que :
- Plus de risques faibles pour A (% en lignes maxi à 46%)
- Plus de risques moyens pour B (% en colonnes maxi à 50%)
- Y a-t-il dépendance entre les 2 stations de ski ?
car de nombreux écarts à l'indépendance sont présents (+ ou - important)
- Indice et dépendance globale
- On calcul le pour l'ensemble
des cases
- Puis on recherche le risque correspondant
nombre de degrés de liberté (d.d.1.)
d.d.l. = (l -1) * (c - 1)
Si >
5% la
différence n'est pas significative au seuil de 5%
Si < ou =
5% la
différence est significative au seuil de
5%
et
- Le degré de
signification est lu dans la table du
(cf.
Table
n°1)
- n'est significatif que si les effectifs calculés
sont > ou
= 5
= [(20 - 69)2/69] + [(100 - 39)2/39] + ... + [(10 -
26)2/26] +
[(80 - 28)2/28] = 385,1
avec d.d.l. = (3 -1) * (3 - 1) = 4
< 1 p.1 000 la
différence est hautement significative
Quand on est dans l'une des modalités de A,
on est pas dans n'importe quelle autre de B
- La liaison est-elle forte ?
- Le calcul du coefficient de Tschuprow est de :
T = {385,1 / 500 * [(3 - 1) * (3 - 1)]^(1/2)}^(1/2) = 0,62
Cette fois si, la liaison est plus nettement significative.
Le risque avalancheux sur une station est assez fortement lié au risque connu sur l'autre
- Peut-on pour autant prédire B connaissant A (ou le contraire) ?
En clair,
- Peut-on supprimer 1 des 2 postes météo
et prédire le risque avalancheux de l'une sur l'autre ?
Cela signifierait qu'il y a concordance entre les modalités des 2 stations
- La concordance* s'observe par une surreprésentation de :
l'effectif observé / l'effectif théorique
sur la diagonale de la matrice
- Est-ce le cas dans l'exemple du risque avalancheux ?
- La concordance se calcule à l'aide d'indices (Kappa de COHEN, K de COLEMAN, ...)
Le Kappa, 
, teste
le degré de concordance formulée sur chaque case concernée
=> sur la diagonale
formule n°8 - (mem51enq.htm)
où :
f(o) => effectif observé dans les cases de la diagonale ;
f(c) => effectif calculé dans les cases de la diagonale ;
les fréquences se calculent indifféremment sur les lignes ou les colonnes
j => le nombre de cases étudiées ;
m => nombre total d'observations.
Le coefficient
varie de - 1 à + 1 :
- 1 concordance inverse (désaccord total)
0 indépendance
+ 1 concordance parfaite
tab. 12 - Exemple de concordance parfaite
observé a b total lignes a 10 0 10 b 0 10 10 total colonnes 10 10 20
calculé a b total lignes a 5 5 10 b 5 5 10 total colonnes 10 10 20
= {[(10 + 10) / 20] - [(5 + 5)
/ 20]} / {1 -
[(5 +
5) /
20]} = 1
(et le
Exemple Avalanches :
= {[(20 + 20 + 80) /
500] - [(69 + 65 +
28) / 500]} / [1 - (69 + 65 + 28)] /
500]
= (0,24 - 0,324) / (1 -
0,324) = - 0,124
- Le
- Il est négatif, le peu de liaison est inverse
Donc on ne peut pas utiliser une station météo pour les 2 stations de ski.
Il n'y a pas concordance
pourtant le test du
- L'analyse du degré de concordance
s'applique aussi aux variables nominales
- Souvent utilisé quand :
- 1 ou plusieurs cases du tableau ont 1 effectif faible ;
- la diversité des modalités n'est pas indispensable
très peu et peu sont regroupées en non favorable
- Comment faire le bon regroupement ?
On classe 200 parcelles en fonction de la nature du peuplement et de l'espacement moyen entre les arbres.
- Existe-t-il une relation entre ces 2 variables ?
tab. 13 - Espacement moyen (3 classes) entre les arbres en fonction de la nature du peuplement
Effectifs observés
Espacement Résineux Feuillus Total lignes < 2,5 m 26 20 46 [2,5 m ; 5 m[ 61 63 124 > 5 m 8 22 30 Total colonnes 95 105 200 Effectifs calculés
Espacement Résineux Feuillus Total lignes < 2,5 m 21,85 24,15 46 [2,5 m ; 5 m[ 58,90 65,10 124 > 5 m 14,25 15,75 30 Total colonnes 95 105 200
= [(26 - 21,85)2
/ 21,85] + [(20 -
24,15)2 /
24,15] + ... + [(8 - 14,25)2
/ 14,25] + [(22 -
15,75)2 /
15,75] = 6,86
avec d.d.l. = (3 -1) * (2 - 1) = 2
Pour 2 d.d.l., la différence est significative
2% <
Son sens est le suivant :
l'espacement le plus élevé se rencontre surout pour les feuillus
- Que ce passe-t-il avec 1 autre découpage ?
Exemple :
Les 200 parcelles précédemment étudiées sont regroupées en 2 classes d'espacement :
- les peuplements denses < 2,5 m
- les peuplements lâches > ou = 2,5 m
tab. 14 - Espacement moyen (2 classes) entre les arbres en fonction de la nature du peuplement
Effectifs observés
Espacement Résineux Feuillus Total lignes < 2,5 m 26 20 46 > ou = 2,5 m 69 85 154 Total colonnes 95 105 200 Effectifs calculé
Espacement Résineux Feuillus Total lignes < 2,5 m 21,85 24,15 46 > ou = 2,5 m 73.15 80,85 154 Total colonnes 95 105 200
= [(26 - 21,85)2
/ 21,85] + [(20 -
24,15)2 /
24,15] + [(69 - 73,15)2
/ 73,15] + [(85 -
80,85)2 /
80,85] = 1,95
Pour 1 d.d.l., la différence n'est pas significative
5% <
La relation entre espacement et nature du peuplement n'est plus significative
pour ce découpage en tout cas
- Les résultats ne sont pas contradictoires
C'est l'illustration provisoire d'un manque de signification
Causes possibles :
- trop petit nombre de sujets ;
- défaut de puissance du test.
Car ici, il restait 2 modalités => perte d'une grande quantité d'info
Récapitulatif : pour une liaison entre 2 variables qualitatives à 2 ou n modalités
1) Établir le tableau croisé des résultats observés
effectifs observés
2) Calcul des effectifs pour 2 variables indépendantes
effectifs théoriques
3) Calculer pour chaque case la différence entre effectifs observés et théoriques
écarts bruts
4) Diviser chaque écart brut par l'effectif théorique
écarts pondérés
5) Repérer et commenter les plus forts écarts pondérés
signe + sur-représentation, attraction
signe - sous-représentation, répulsion
6) Calculer et tester la significativité de la liaison
7) Calculer l'intensité de la liaison
T de Tschuprow par exemple
8) Recherche du degré de concordance (si nécessaire)
- Repérer les cases où l'on attend des surreprésentations
- Calculer la somme des effectifs observés sur les cases intéressantes
diviser la par l'effectif total
- Calculer la somme des effectifs calculés de ces cases
diviser la par l'effectif total
- Calculer le coefficient Kappa,
|
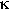
Communiquez-moi par courrier électronique les réponses aux questions suivantes Question n°5.1.1. La table de contingence renseigne sur :
Question n°5.1.2. Si la valeur du khi2 lue dans la table dépasse celle calculée :
Question n°5.1.3. Le test du khi2 permet de se prononcer sur le rejet ou l'acceptation de :
|
NB : les mots suivis de "*" font partie du vocabulaire statistique, donc leur définition doit être connue. Faites-vous un glossaire.