On pourra lire à ce sujet le roman de Denis Guedj "Les Cheveux de Bérénice" publié en janvier 2003 aux Éditions du Seuil.
fig. 1 - La mesure du rayon terrestre par Ératosthène
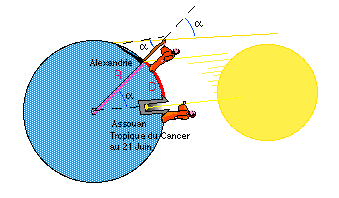
Sources : www.ign.fr
V.2.5 - Dernière mise à jour : 30/11/2022
La Terre est une sphère
Les globes en sont l'unique représentation fidèle
Mais pour des raisons pratiques
on préfère utiliser des planisphères ou des mappemondes (désuet)
- Avantage : se plient et se transportent partout même à grande échelle
- Inconvénient : ce sont des surfaces courbes qui ne peuvent être représentées à plat sans déformations
Pour passer d'une sphère à un plan on va pratiquer une projection
Pour commencer, une petite vidéo de 26 min qui commence à être historique (1999) : C'est pas sorcier - Cartographie
Les formes de la Terre s'étudient au travers de la géodésie*
Qu'est-ce que la géodésie ?
Cette vidéo de l'IGN apporte un début de réponse.
C'est le savant grec Ératosthène vers 240 avant JC qui a fait la première mesure du rayon de la Terre.
On pourra lire à ce sujet le roman de Denis Guedj "Les Cheveux de Bérénice" publié en janvier 2003 aux Éditions du Seuil.
fig. 1 - La mesure du rayon terrestre par Ératosthène
Sources : www.ign.fr
- L'hypothèse d'une terre légèrement aplatie selon l'axe des pôles date du XVIIIe siècle.
fig. 2 - Triangulation le long de la méridienne
Sources : www.ign.fr
Ce sont des campagnes de triangulation* (mesures d'angles et de distances) :
- entre Dunkerque et les Pyrénées (Méridien de Cassini) ;
de nombreuses améliorations sont apportées par des campagnes successives, notons :
- l'abbé Picard sous Louis XIV ;
- à la révolution, l'expédition Méchain-Delambre...
On pourra lire à ce sujet le roman de Denis Guedj "Le Mètre du monde" publié en janvier 2000 au Seuil ou "La méridienne" en 1999 chez Robert Laffont.
- en Laponie (mesures d'arc méridien vers le pôle nord, expédition Maupertuis) ;
- au Pérou (mesures d'arc méridien vers l'équateur, expédition La Condamine).
qui permettront de passer d'un sphéroïde à un ellipsoïde*.
- En France, des campagnes de triangulation de plus en plus précises ont permis de déterminer trois réseaux de points successifs couvrant tout le territoire national. Ils sont associés à trois cartes de plus en plus détaillées :
- Triangulation des Cassini => carte de Cassini du XVIIIe siècle (échelle du 1/86 400) ;
- Triangulation des Ingénieurs Géographes => carte d'État-Major au XIX e siècle (échelle du 1/80 000) ;
- Nouvelle Triangulation de la France (NTF) => Série bleue IGN (échelle du 1/25 000).
D'autres techniques contribuent à la connaissance des formes du globe :
- Le nivellement* => connaissance de l'altitude des points d'un réseau par rapport au niveau moyen des mers.
environ 450 000 points
- La gravimétrie* => connaissance de la forme du champ de pesanteur (géoïde) et de ses irrégularités par rapport à l'ellipsoïde.
- La NTF a été achevé en 1991.
- Elle comporte 80 000 points
- C'est un réseau local*
- Mais depuis décembre 2000, le RGF 93 (Réseau Géodésique Français) est devenu le système légal français :
- C'est un réseau spatial*
- Il est compatible avec les systèmes européens.
On consultera avec intérêt le lien suivant : Géoïde in Wikipédia (bcp plus complète en anglais)
Pour comprendre le géoïde => voir la vidéo Les Marées et le mouvement lunaire
Celle de l'IGN est également très instructive.
fig. 3/23 - Relation géoïde-ellipsoïde (gfm21f23.gif)
Sources : BTS Géomètre
La Terre a une forme irrégulière.
- Pour l'appréhender, les géodésiens ont défini une surface théorique : le géoïde*.
- Sa forme visible est le niveau moyen des mers
- Sa définition relève de l'analyse gravimétrique
- Le géoïde caractérise une surface où la gravité est constante : équipotentielle.
- L'océan est une surface équipotentielle.
- Un des satellites d'altimétrie spatiale, Topex-Poséidon, permettait (1992-2005) de mesurer :
Il a été remplacé par la série des satellites franco-américains Jason.
fig. 3/22 - Le satellite
Topex-Poséidon et les mesures altimétriques
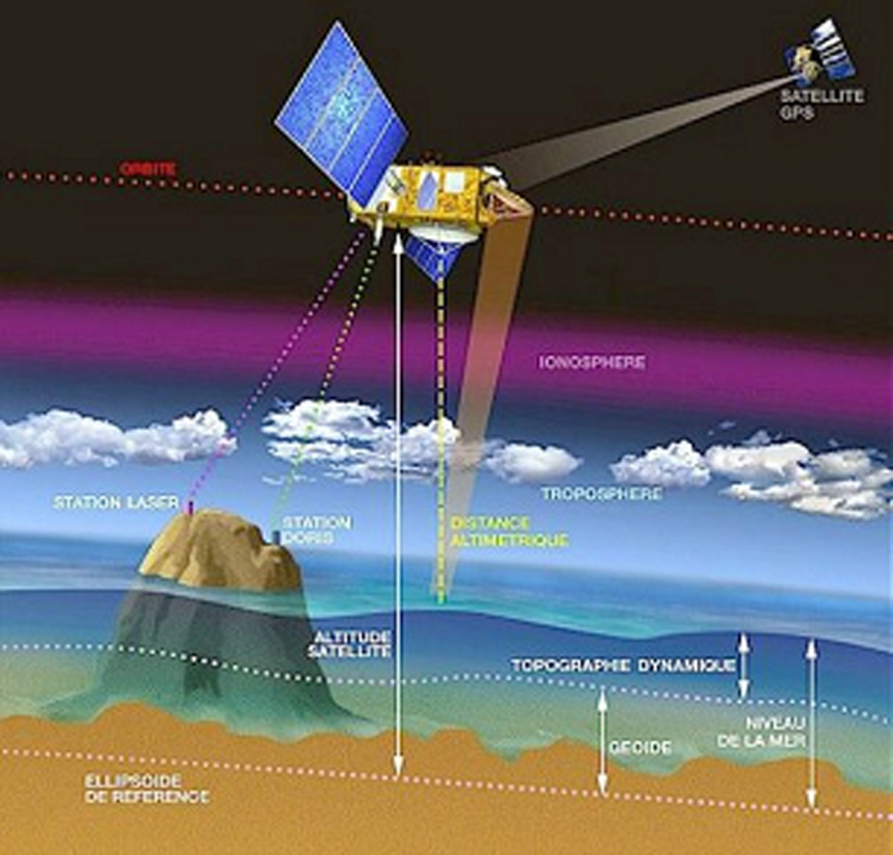
Sources : ENSG
- Le géoïde ressemble à une sphère aplatie aux pôles
fig. 3 - Le géoïde et les ellipsoïdes
Sources : www.ign.fr
Le modèle mathématique le plus proche du géoïde est
un ellipsoïde de révolution*
Il existe de nombreux modèles d'ellipsoïdes.
Certains sont à :
- référence locale
exemple :
NTF => ellipsoïde associé => Clarke 1880
ED50 => ellipsoïde associé => Hayford 1909
d'autres à
- référence spatiale (globale)
exemple :
WGS 84 => ellipsoïde associé => WGS84 (celui du GPS)
RGF93 => ellipsoïde associé => IAG-GRS80
Sources : ellipsoide_geodesique.pdf, doc. IGN
- Les systèmes locaux, les plus anciens, sont :
- issus de réalisations terrestres ;
- positionnés à quelques centaines de mètres du centre des masses de la Terre.
Les systèmes spatiaux, les plus récents :
- sont mondiaux ;
- ont leur origine située à quelques mètres du centre des masses de la Terre.
fig. 3/21 - Centres distincts d'ellipsoïde de révolution (gfm21f21.gif)
Sources : webzoumine, (selon les sources, l'ED50 est associé à l'ellipsoïde Hayford 1909 ou 1924, en raison de la date du congrès de Madrid qui l'a adopté, sur le site de l'IGN, c'est 1909)
Ces ellipsoïdes ont
- des centres distincts ;
- des dimensions différentes.
Les surfaces décrites par chaque ellipsoïde ne sont pas jointives.
Un point donné y aura donc des coordonnées différentes.
Cependant, des formules mathématiques permettent de passer d'un système géodésique à l'autre avec des résultats variables en précision selon qu'on est au centre ou en périphérie de la surface.
- Un système géodésique* est un repère affine* (qui accepte des transformations linéaires) tel que :
- l'origine O est proche du centre des masses (de gravité) de la Terre ;
- l'axe OZ est proche de l'axe de rotation de la Terre ;
- le plan OX, OY est proche du plan équatorial ;
- le plan OX, OZ est le plan méridien origine.
fig. 4 - Le repère affine
Sources : www.ign.fr
Ce sont les coordonnées tridimensionnelles dans ce repère géodésique qui permettent de positionner un point à la surface de la Terre.
Si l'on veut connaître sa position en coordonnées géographiques, il faut associer à ce repère un ellipsoïde (modèle géométrique des formes de la Terre, mais sans les reliefs)
- Donc, un ellipsoïde centré en O est associé à ce repère.
Il a pour dimension :
- le demi grand axe => a ;
- le demi petit axe => b ;
- l'inverse de l'aplatissement =>
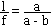
- la première excentricité =>
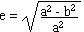
Pour voir un exemple calculé sur le WGS 84
- À chaque référentiel géodésique est associé un ellipsoïde.
Il existe, en général, plusieurs ellipsoïdes de référence valables pour une région donnée :
Par exemple :
- en France, les ellipsoïdes utilisés s'approchent au plus près du géoïde en France (cf. tab. 1) ;
- idem pour ceux des systèmes géodésiques européens (ED50 basé sur l'ellipsoïde de Hayford, le WGS84 basé sur l'ellipsoïde WGS84, ou le RGF93 sur l'IAG-GRS80) ;
- en amérique du Nord : le NAD27 basé sur l'ellipsoïde de Clarke 1866 ou le NAD80 sur l'IAG-GRS80 - Sources : Statistique Canada).
tableau n°1 - Modèles d'ellipsoïdes en usage en France
Sources : www.ign.fr et NGA pour le WGS84
Système
géodésiqueEllipsoïde
associéa
b
1/f
e
NTF Clarke 1880 IGN 6378249.2 6356515.0 293.466021 0.08248325676 ED50 Hayford 1909 6378388.0 6356911.9461 297.000000 0.08199188998 RGF93 IAG-GRS80 6378137.0 6356752.314 298.257222 0.08181919106 WGS84 WGS84 6378137.0 6356752.3142 298.257223 0.08181919084 fig. 5 - Formes d'ellipsoïdes en usage en France
Sources : www.ign.fr
- Le méridien origine
- est défini par le plan OX/OZ ;
- peut être celui de Greenwich => méridien international* ;
- peut être propre à la géodésie d'un pays => méridien de Paris pour la France ;
- est compté positivement vers l'est ;
- est défini numériquement par rapport au méridien international.
Le méridien de Paris est à 2° 20´ 14.025" à l'est de celui de Greenwich.
Au XXe siècle, grâce aux progrès :
- des mesures électromagnétiques ;
- de la puissance de calcul de l'informatique ;
- de la gravimétrie ;
- de l'astrogéodésie ;
- des méthodes spatiales, ...
nous avons affiné notre connaissance de la forme de la terre, du géoïde.
Parallèlement, la géodésie spatiale a établi des réseaux qui ceinturent la terre et donnent un positionnement absolu et relatif en coordonnées géocentriques.
- Qu'est-ce que les coordonnées (cf. fig. n°4) ?
- Les coordonnées peuvent être exprimées sous la forme de :
- Coordonnées cartésiennes géocentriques (x, y, z)
- Coordonnées
géographiques ![]()
- en représentation plane (coordonnées dites en "projection")
- elles sont prises par rapport au centre de la Terre ;
- elles correspondent à la projection du point M sur les axes (x, y, z) ;
- c'est le système initial du positionnement par satellite ;
- mais elles servent surtout comme intermédiaire de calcul dans les changements de systèmes géodésiques de référence.
- la lettre grecque
(lambda) désigne la longitude ;
- la lettre grecque
(phi) désigne la latitude ;
- la lettre h correspond à la hauteur ellipsoïdale (à ne pas confondre avec l'altitude). Elle est définie dans un système de référence géodésique et peut différer de l'altitude de plusieurs dizaines de mètres (si vous voulez en savoir plus, explorez ma source : CERTU RGF93_theorie_et_concept_T1.pdf).
fig. 5.1 - Altitude et hauteur ellipsoïdale
Sources : BTS GéomètreH est l'altitude ;
C est la distance "normale" entre l'ellipsoïde et le géoïde ;
h la hauteur ellipsoïdale (valeur fournie par les récepteurs GPS pour le "z", qui peut donc être différente de l'altitude !)
On peut voir sur la figure 5.2 la différence calculée par l'IGN entre le géoïde et l'ellipsoïde de l'ancien système de référence français, la NTF. Je n'ai pas encore d'illustration pour le RGF93.
fig. 5.2 - Corrections à apporter à l'altitude (Géoïde) pour obtenir la hauteur ellipsoïdale (par rapport au NGF)
Sources : BTS Géomètre
- Quelles sont les unités des coordonnées géographiques ?
tableau n°2 - Notation des unités angulaires pour les latitudes et longitudes
degrés, minutes, secondes sexagésimaux (dit DMS)
° ´ " degrés, minutes décimales ° ´ degrés décimaux (dit DD)
° grades (ou gon) gr radians rd Un degré de longitude équivaut à environ 111 km sur l'équateur mais ne vaut plus que 74 km à une latitude de 48 degrés et devient 0 km au pôle Nord.
- Comment calculer des distances avec
des coordonnées géographiques ?
Lorsque les distances sont grandes (en dehors d'une coupure au 1/25 000 par exemple), la méthode préconisée repose sur de la trigonométrie sphérique (¯\_(ツ)_/¯ !) ! Voir le développé théorique ici : https://geodesie.ign.fr/contenu/fichiers/Distance_longitude_latitude.pdf
On passe par les grands cercles de la Terre pour ne pas passer au travers de celle-ci comme avec les distances euclidiennes et raccourcir la distance réelle.
Vous trouverez ici trois méthodes pour calculer la distance entre deux points connus en degrés décimaux : http://villemin.gerard.free.fr/aGeograp/Distance.htm
Deux sont développées ici (gfm21ta7.xlsx), dans une feuille de calculs Excel pour effectuer quelques essais. Essais que l'on pourra comparer avec des transformateurs trouvés sur Internet.
Pour ce qui est des ordres de grandeur pour la France (voir le figure n°7)
fig. 7 - Longueurs en km d'un degré de longitude (mesuré sur les parallèles) en France métropolitaine
Sources : http://villemin.gerard.free.fr/aGeograp/Distance.htm
Rappelons que le degré de longitude fait environ 111 km à l'équateur !
Et que le degré de latitude fait toujours environ 111 km (111.195 km)
- Comment localiser des positions avec des coordonnées géographiques issues de référentiels différents?
tableau n°3 - Un même point, mais des coordonnées angulaires différentes !
Sources : ESRI in : Généralités sur les systèmes de coordonnées
Système de coordonnées géographiques
NTF (méridien de Paris)
NTF (méridien de Greenwich)
ED50 (Greenwich)
WGS84 (Greenwich)
Longitude
5°24´0" Est
7°44´14,0" Est
7°44´16,4" Est
7°44´12,2" Est
Latitude
48°36´00,0" Nord
48°36´00,0" Nord
48°36´03,0" Nord
48°35´59,9" Nord
- Où est-ce ? Lequel de ces points pouvez-vous placer sur le Géoportail ? sur Google Map ?
- Quel est le système de coordonnées dans Google Map ?
- Comment convertir des degrés sexagésimaux en degrés décimaux et vice versa ?
Voir ici : Système sexagésimal
Une vidéo sur les coordonnées géographiques et les altitudes
- conventionnellement, les coordonnées en projection sont E et N (Est, Nord) pour éviter toute confusion avec les coordonnées cartésiennes (x, y, z) ;
- permet de représenter par une surface plane une partie du modèle ellipsoïdal ;
- permet d'utiliser des valeurs métriques plus faciles à exploiter que les valeurs angulaires.
tableau n°4 - Un même point, mais des coordonnées projetées différentes !
Sources : ESRI in : Généralités sur les systèmes de coordonnées
Système de coordonnées projetées X Y NTF - Lambert I Zone 997 960 m
114 185 m
NTF - Lambert II Etendu 998 137 m
2 413 822 m
ED50 - UTM fuseau 32 Nord 406 946 m
5 383 958 m
WGS84 - UTM fuseau 32 Nord 406 864 m
5 383 757 m
RGF93 - Lambert 93 1 049 052 m
6 843 777 m
- A quels chiffres s'attacher pour déterminer le système de coordonnées ?
fig. 6 - Cohabitation de deux systèmes de coordonnées
Sources : ESRI
- Pour les cartes françaises, les coordonnées s'expriment :
- en degrés sexagésimaux et en coordonnées planes UTM (kilométriques) ;
Système européen ED50
- en grades et en coordonnées planes Lambert (kilométriques) ;
Système NTF (Nouvelle triangulation française)
- de plus en plus en coordonnées planes UTM rapportées aux systèmes RGF93 ou WGS84 (kilométriques) ;
Système RGF (Référentiel géodésique français)
Système WGS (World Geodetic System)
Seulement, il n'existe pas de projections sans déformations.
|
Communiquez-moi sur la plateforme Moodle, à la rubrique "Questions de cours", les réponses aux questions suivantes :
Question n°2.1.1. La NTF est issue d'un réseau :
Question n°2.1.2. Combien d'ellipsoïdes de révolution (modèles mathématiques) correspondent au géoïde (surface théorique) :
Question n°2.1.3. Les coordonnées kilométriques lambert sont des coordonnées :
Question n°2.1.4. La hauteur se calcule par rapport :
|
NB : les mots suivis de "*" font partie du vocabulaire géographique, donc leur définition doit être connue. Faites-vous un glossaire.