Vincent GODARD
Département de Géographie
Université de Paris 8
V.1.2.1 - Dernière mise à
jour : 19/10/2016
Fiche Mémo n°4.1. du cours de Statistique :
Les mesures de la dispersion statistique
Elles mesurent l'hétérogénéité d'un caractère
C'est-à-dire, si la
distribution est concentrée ou
non
autour d'une valeur centrale
- Ne pas confondre dispersion statistique et
géographique
Leur signification est opposée
:
- La dispersion statistique est grande lorsque
la dispersion géographique est
minimale (concentration spatiale)
fig. 1 - Dispersion statistique forte /
Dispersion géographique faible
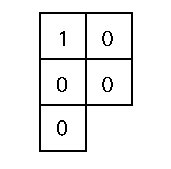
- La dispersion
statistique est faible lorsque
la dispersion géographique est
maximale (dispersion spatiale =
phénomène uniformément réparti)
fig. 2 - Dispersion statistique faible /
Dispersion géographique forte
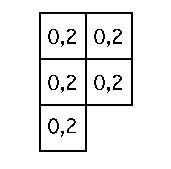
- La dispersion statistique
peut être absolue ou relative
1. La dispersion absolue
La dispersion absolue est
exprimée dans l'unité de mesure du
caractère
1.1. Caractéristiques de dispersion ne tenant pas compte
d'une valeur centrale
Elles n'utilisent pas explicitement une valeur
centrale pour être déterminées
1.1.1. L'étendue
Synonyme : amplitude*
C'est un intervalle de variation*
(en anglais range)
E = xi max - xi min
- Inconvénient : ne
dépend que des valeurs extrêmes
Il n'est donc pas toujours
significatif
- Il
faut limiter l'emploi de l'étendue* aux séries dont on
reconnaît une signification aux valeurs extrêmes
comme
certains paramètres climatiques
tels que :
l'amplitude thermique
annuelle
Où les extrema sont déjà des
valeurs lissées (des moyennes) écrêtées
des irrégularités annuelles
- L'étendue est également
très utilisée pour discrétiser une série
1.1.2. L'écart interfractiles ou
interquantiles
Synonyme : intervalle interfractiles* ou
interquantiles*
- Les quantiles ou fractiles sont des
paramètres de
position
Mais, l'écart interquantile est
un paramètre de
dispersion absolue
L'écart
interquantile est une étendue au sein de la
série
- Les 2 plus connus sont :
- L'intervalle de
Kelley (Ik)
Ik = D9 - D1
- comprend 80 p.100 de
l'effectif
- permet d'éliminer les valeurs
extrêmes
(par exemple : les
pluviométries exceptionnelles)
- L'intervalle
interquartile (IIQ)
IIQ = Q3
- Q1
- comprend 50 p.100 de l'effectif
- permet de ne travailler que sur le centre de la
série
(par exemple : les classes
moyennes)
L'écart
interquantile permet des mesures d'étendue
partielle
- L'approche visuelle de la dispersion par
l'écart
interquantile,
passe par le diagramme en Boite et
Moustaches (ou Box plot)
1.1.3. Analyse d'un 1er exemple
Reprendre l'exemple du Tableau 1
(mem32sta.htm) - PIB par habitant des
régions de France, d'Italie et d'Espagne en 1991 -
(Sources : Eurostat, 1992, in SAINT-JULIEN
1999, p.23).
Téléchargement
du tableau
Ce fichier est au format EXCEL 5.0 et "pèse" 97 Ko.
Calculer pour l'Europe du sud, feuille :
Tab1b
- l'étendue
- l'intervalle interquartile
1.2. Caractéristiques de dispersion tenant compte d'une
valeur centrale
1.2.1. L'écart-moyen absolu et
l'écart-médian absolu (écart probable)
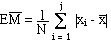 formule
n°1 (mem41sta.htm)
formule
n°1 (mem41sta.htm)
Avec :
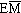 l'écart à la moyenne arithmétique
;
l'écart à la moyenne arithmétique
;
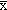 la moyenne arithmétique ;
la moyenne arithmétique ;
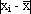 l'écart, en valeur absolue, à
la moyenne arithmétique ;
l'écart, en valeur absolue, à
la moyenne arithmétique ;
N l'effectif total,
la somme des ni.
et pour les distributions groupées
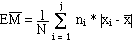 formule
n°2 (mem41sta.htm)
formule
n°2 (mem41sta.htm)
Avec :
xi qui devient le centre de
classe ;
ni effectif de la
modalité i ;
j le nombre de
modalités.
L'écart à la
moyenne conserve l'unité de la série
- Les applications les plus usuelles sont d'ordre
:
- cartographique
- climatologique
Exemple n°2 :
Reprendre le Tableau 2
(mem24sta.htm) - Distribution des
précipitations en Mauritanie entre 1940 et 1990 -
(Sources : ASECNA, ORSTOM).
Téléchargement
du tableau
Ce fichier est au format EXCEL 5.0 et "pèse" 97 Ko.
- Calculer les écarts à la moyenne
pour chaque station
- Puis calculer :
- la moyenne moins un écart
à la moyenne ;
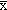 -
-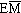
- la moyenne plus un écart à la
moyenne ;
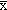 +
+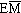
- Tracer les trois courbes en trois graphiques
séparés ;
- Reporter les droites :
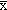 -
-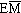
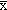 +
+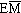
pour chaque station.
- Quelles sont les
années excédentaires ?
- Quelles sont les
années déficitaires ?
- De combien d'écart
à la moyenne ?
- Il en va de même pour
l'écart-médian absolu
- Cet écart correspond à la
médiane des écarts
- il y a 50 p.100 des écarts de
part et d'autre de l'écart-médian absolu
-il se calcule en remplaçant la moyenne par
la médiane (of
course !)
1.2.2. L'écart à la moyenne élevé au
carré (variance et écart-type)
1.2.2.1. La variance
La variance* notée
(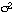 ) est la moyenne
arithmétique des carrés des écarts à la
moyenne.
) est la moyenne
arithmétique des carrés des écarts à la
moyenne.
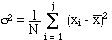 formule
n°3 (mem41sta.htm)
formule
n°3 (mem41sta.htm)
et pour les distributions groupées
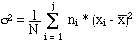 formule
n°4 (mem41sta.htm)
formule
n°4 (mem41sta.htm)
Avec :
xi qui devient le centre de
classe ;
ni effectif de la
modalité i ;
j le nombre de
modalités.
Le carré de
l'écart à la moyenne donne un résultat non nul
et positif.
- Prendre le
carré des écarts à la moyenne
c'est :
renforcer le poids
des valeurs extrêmes
donc notre perception de la dispersion
De ce fait, les valeurs
extrêmes ont un poids :
- majoré dans le calcul de
la dispersion absolue par la
variance
- minoré par l'utilisation
des quantiles
L'utilisation de la variance
est conditionnée par une distribution
proche d'une distribution normale,
dont la forme est
une courbe
en cloche sans
asymétrie
Il faut donc contrôler la forme de la
distribution
1.2.2.2. L'écart-type
Synonyme : écart quadratique moyen ou déviation
standard
L'écart-type* est
noté ( ) c'est la racine carrée de la variance
) c'est la racine carrée de la variance
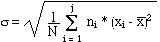 formule
n°5 (mem41sta.htm)
formule
n°5 (mem41sta.htm)
Note :
- l'écart moyen absolu est égal
à l'écart-type dans le cas d'une distribution gaussienne*
c'est donc très rare en géographie
- ne pas confondre dans EXCEL (et dans une moindre
mesure pour les calculettes) les fonctions :
ECARTYPE
calculées sur un
échantillon
ECARTYPEP
calculées sur l'ensemble de la
population
- la variance est un
intermédiaire de calcul sans valeur
descriptive concrète
l'écart-type
est son expression descriptive
lui seul porte l'unité de mesure de cette
variable
- l'écart-type est la
caractéristique de dispersion la
plus courante
Pourtant, il n'est pas toujours
adapté à la forme de la distribution
Mais, il a une valeur probabiliste dans les
distributions
normales.
1.2.3. Suite du 1er exemple
Reprendre l'exemple du Tableau 1
(mem32sta.htm) - PIB par habitant des
régions de France, d'Italie et d'Espagne en 1991 -
(Sources : Eurostat, 1992, in SAINT-JULIEN
1999, p.23).
Calculer pour l'Europe du sud, feuille :
Tab1b
- l'écart moyen absolu
- l'écart-type
- Quels sont les avantages
respectifs et les limites de l'étendue, de l'intervalle
interquartile, de l'écart moyen absolu et de
l'écart-type ?
2. La dispersion relative
La dispersion relative sert
à comparer plusieurs distributions
- Elle permet d'éliminer les
problèmes
:
- d'échelle lors de
comparaison de distributions trop différentes ;
- d'unités de mesures
lorsque les distributions sont "incompatibles".
- Les
caractéristiques de dispersion relative sont :
- en général
des
quotients (caractéristique de
dispersion absolue / valeur centrale)
- toujours sans unité, voire exprimées en %.
Enfin, il est préférable que la
variable soit :
- positive
- dotée d'une
origine non arbitraire
Par exemple, il est
préférable d'avoir 0 °K plutôt que 0 °C
(273 °K) !
sinon il faut réaliser des transformations
pour rendre les calculs cohérents.
2.1. Relativisation sans référence à une
valeur centrale
Une seule courante : Le minimax
- Mêmes
qualités et les mêmes défauts que
l'étendue :
sa
référence aux extrema de la distribution
- C'est le rapport entre
le maximum et le minimum de la distribution
Le minimax = xi max / xi min
Très utilisée pour comparer des
salaires d'une entreprise à l'autre
2.2. Relativisation par rapport à une valeur centrale
2.2.1 Le coefficient de variation
C'est la plus connue
Le coefficient de
variation* est noté (CV), il se calcule comme suit :
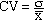 formule
n°6 (mem41sta.htm)
formule
n°6 (mem41sta.htm)
Note :
- Il est souvent exprimé en % (CV *
100)
- Si le coefficient de
variation est
égal à 18 %
cela signifie que l'écart-type vaut 18 % de la
moyenne
- Le coefficient de
variation est très sensible
à la valeur de la moyenne
Plus la moyenne est proche de 0
moins le CV est
exploitable, car il tend vers l'infini
2.2.2 Les coefficients interquantiles
Le plus connu est le coefficient interquartile
Le coefficient
interquartile* est noté (CIQ), il
se calcule comme suit :
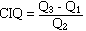 formule
n°7 (mem41sta.htm)
formule
n°7 (mem41sta.htm)
c'est l'intervalle
interquartile divisé par la médiane
Note :
- La variabilité
relative est donc proportionnelle à la valeur
centrale
- Ces coefficients peuvent être
difficilement
interprétables dès que
:
la moyenne et la
médiane sont proches de 0
- Ces coefficients ont
l'inconvénient de ne pas avoir de limite
supérieure
2.2.3. Suite du 1er exemple
Reprendre l'exemple du Tableau 1
(mem32sta.htm) - PIB par habitant des
régions de France, d'Italie et d'Espagne en 1991 -
(Sources : Eurostat, 1992, in SAINT-JULIEN
1999, p.23).
- Pour chaque pays, caractériser la
distribution du PIB par habitant à l'aide (feuille : Tab1c)
:
- de la moyenne
- de l'écart-type
- du coefficient de variation
- Quel est le pays le plus
homogène pour le PIB par habitant ?
- Quel est le pays où ce
caractère induit les plus fortes disparités
?
- Réaliser le découpage des
écarts à la moyenne globale du PIB qui tienne compte
:
- de la moyenne comme limite de classe ;
- de l'écart-type comme
amplitude de
classe.
- Construire le tableau de dénombrement
issu de ce découpage
- Représenter la distribution à
l'aide d'un diagramme en barres (fonction histogramme d'EXCEL)
- Est-elle en
cloche ?
- Réaliser une carte à l'aide du
découpage précédent
Téléchargement
du fond de carte
(Sources : Code et localisation des régions de France,
d'Italie et d'Espagne, in : SAINT-JULIEN
1999, p.25).
Ce fichier est au format ".TIF" et "pèse" 290 Ko.
- Quelle analyse faites-vous de
cette carte ?
- Quelles différences
voyez-vous entre cette carte et les mesures de dispersion
?
- Quelles différences
voyez-vous entre cette carte et la cartographie de la variable
elle-même ?
3. Test de compréhension
|
Communiquez-moi par
courrier
électronique les réponses aux questions
suivantes
Question
n°4.1.1. Quel
paramètre de dispertion tient compte d'une valeur
centrale :
a) l'étendue
b) l'écart-médian
absolu
Question n°4.1.2.
Quel paramètre de
dispertion absolue est combiné à la moyenne
pour calculer le coefficient de variation :
a) l'écart-moyen
absolu
b) l'écart-type
Question n°4.1.3.
En cas de distribution
asymétrique, il est préférable
d'utiliser :
a) le coefficient de
variation
b) le coefficient interquartile
Précisez à la rubrique objet
:
EC
statistique
puis dans le
corps du message vos
n°
d'étudiant, nom et prénom
puis vos
réponses
vgodard@univ-paris8.fr
|
Retour au début de la fiche
Mémo
Fiche Mémo suivante
NB : les mots suivis de "*" font
partie du vocabulaire statistique, donc leur définition doit
être connue. Faites-vous un glossaire.

