Sources : Dumolard
2005, p. 3
V.1.4.5 - Dernière mise à jour : 15/10/2019
Note : mon précédent cours d'analyse de données multivariées devait beaucoup à l'ouvrage de Léna Sanders, maintenant épuisé (sauf en bibliothèques, mais téléchargeable ici). Celui-ci s'inspire, en plus, pour la forme et pour certains exemples de celui de Pierre Dumolard. Qu'ils soient ici tous les deux remerciés pour leur contribution (involontaire ;-) !)
Groupes de techniques permettant :
- de traiter simultanément un ensemble nombreux de variables ;
- de ne pas faire d'hypothèses contraignantes a priori ;
- de faire ressortir une structure latente, profonde, non immédiatement décelable ;
- de simplifier et d'organiser l'information.
1) Analyse spatiale des données ou analyse des données spatiales ?
Ici, on ne s'occupera qu'a posteriori des contraintes spatiales !
Par exemple :
1) réalisation d'une typologie
2) représentation cartographique de la typologie
3) analyse spatiale de sa répartition
2) Quid de la notion d'indépendance des données ?
La culture disciplinaire prime sur l'outil.
Cependant, pour révéler le contenu sous-jacent de vos données, il est préférable d'avoir fait un peu de (et compris l'intérêt de la) :
- statistique univariée, typiquement le cours de statistique de L2 et en particulier : "2. Les valeurs centrales" ; "3. Les paramètres de dispersion"
- statistique bivariée, typiquement le cours d'enquête de L3 et en particulier : les "5. Analyses bivariées" entre caractères qualitatifs, quali/quanti et quantitatifs.
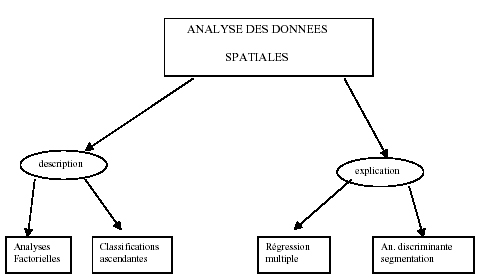
Ceci mis à part, deux grandes familles d'analyse multivariée sont abordées pendant ce cours :
- les analyses plutôt descriptives (ACP, AFC, classifications...)
- les analyses dites explicatives (régressions multiples, segmentations...)
fig. 1b - Les deux grandes familles d'analyse multivariée
Sources : Dumolard 2005, p. 3
- Parmi les méthodes descriptives (celles qui seront prioritairement pratiquées ici), on distingue deux grands groupes en fonction de leur finalité.
Ceux qui servent plutôt à :
- former des groupes de variables et à hiérarchiser l'information ;
=> analyses factorielles*
et ceux qui servent plutôt à :
- former des groupes d'individus ;
=> classifications multivariées*
- L'ensemble de ces méthodes est adapté à l'analyse de l'organisation de l'espace
- Ces méthodes nécessitent :
- une organisation de l'information géographique en matrice d'information spatiale* ;
- une réflexion sur le choix des unités spatiales élémentaires* (nature et échelle du problème traité) ;
- une réflexion sur le choix des variables* (homogénéité de l'information).
- Ces méthodes ne supposent pas :
- d'hypothèses sur la distribution statistique des variables (pour certains auteurs seulement ! Voir plus loin.) ;
- ni de connaissances de modèles probabilistes particuliers ;
contrairement aux méthodes classiques de la statistique.
- Quelles que soient les dimensions de la matrice d'information :
- Ces méthodes descriptives servent à :
- affiner les descriptions ;
- éliminer les "bruits" qui parasitent notre perception ;
- révéler les associations et les interactions ;
- éliminer la part d'arbitraire des comparaisons de cartes.
Donc à réaliser des typologies*
C'est à dire, constituer des groupes d'individus plus semblables entre eux qu'ils ne le sont avec les autres (au regard des variables étudiées).
- Une analyse factorielle sert à :
- résumer ;
et
- hiérarchiser ;
l'information contenue dans un tableau numérique de :
- n lignes (les individus) ;
- p colonne (les variables).
Les n individus sont décrits par un nuage de points dans p plans [les p variables (soit p plans !)].
Exemple :
Prenons les 20 arrondissements de Paris (n = 20 individus) et les recensements de 1990 et 1999 (p = 2 variables) ;
Le tableau de 20 lignes (1 par arrondissement) et deux colonnes (1 par recensement) sur un graphique à deux dimension formera un nuage de points de coordonnées x = population de l'arrondissement en 1990 et y = population de l'arrondissement en 1999.
- L'information représentée par ce nuage,
c'est la dispersion des n points.
- Produire un résumé de cette information c'est
projeter ces points dans un espace de dimension inférieure à p.
Exemple :
Prenons les 20 arrondissements de Paris (n individus) et les 33 recensements (p variables) ;
Cela donne un tableau de 660 "informations", soit 660 intersections possibles (20 * 33)
Pour l'analyser, il faut le résumer !
Passer de 33 variables à 2-3 néo-variables concentrant l'information d'origine serait une "bonne" opération cognitive !
C'est l'objectif de l'analyse multivariée
- Les axes de ce sous-espace sont dits "axes factoriels*" ou "facteurs*".
- Le résumé est possible dans la mesure où
les variables ne sont pas totalement indépendantes
- Chaque variable "p" porte en elle :
- une part d'information originale ;
- une part d'information redondante avec les autres.
C'est cette part d'information redondante que l'on va regrouper dans le résumé factoriel.
- Chaque facteur est la combinaison linéaire des "p" variables.
A chaque variable est associé un coefficient "a".
Ce coefficient "a" est proportionnel à l'intensité qui lie la variable au facteur.
Ces facteurs, ou axes, rendent compte des associations entre les variables.
Leur nombre apparaît bien plus réduit que celui des variables d'origine.
Les facteurs sont hiérarchisés :
- le 1er axe concentre le maximum de l'information ;
- c'est l'axe de la plus grande dimension du nuage de points
- c'est le meilleur résumé dans un espace à une dimension
- mais il laisse des résidus (de l'information)
- le 2e axe concentre le maximum de l'information restante ;
- il est orthogonal au premier (par construction)
- c'est l'axe de la plus grande dimension résiduelle du nuage de points
- associé au 1er axe, c'est le meilleur résumé dans un espace à deux dimensions
- mais il laisse aussi des résidus
- le 3e axe prend encore une part d'information moindre ;
- il est orthogonal au deux premiers (toujours par construction)
- ainsi de suite
Objectif principal : former et hiérarchiser des groupes de variables
- L'analyse en composantes principales (ACP)
C'est la technique la plus ancienne
- S'applique principalement aux tableaux de mesures*
=> variables quantitatives (données brutes, ratio, %, ...)
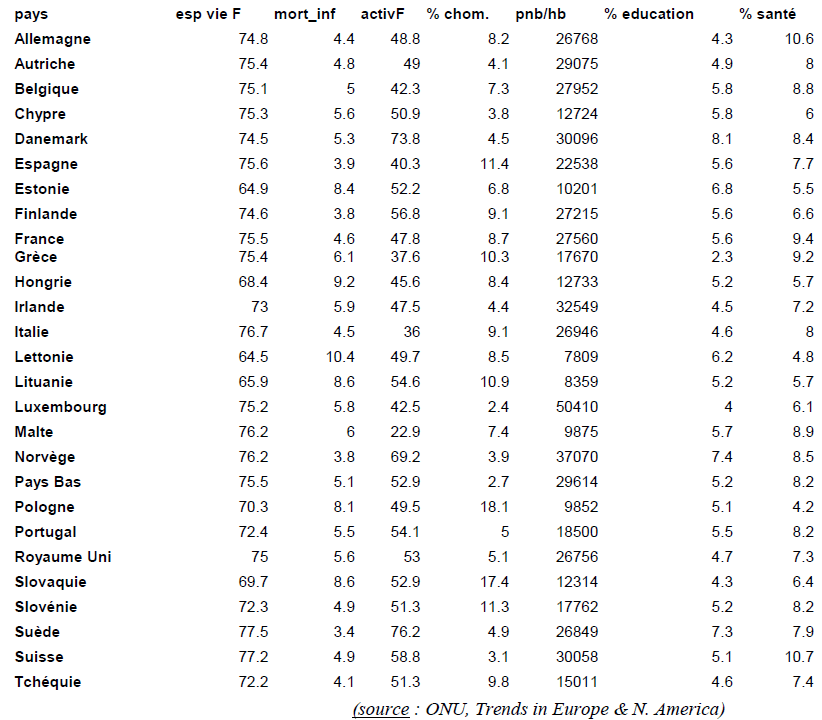
tab. 1 - Variables démographiques et économiques pour 27 pays européens (DUMOLARD 2005, tab. 2.2) => matrice d'information spatiale
- l'Analyse factorielle des correspondances (AFC)
- S'applique principalement aux tableaux de contingence*
=> variables quantitatives (données brutes sommables en lignes et en colonnes)
- Mais également aux tableaux disjonctifs complets*
=> variables qualitatives (nominales en présence / absence)
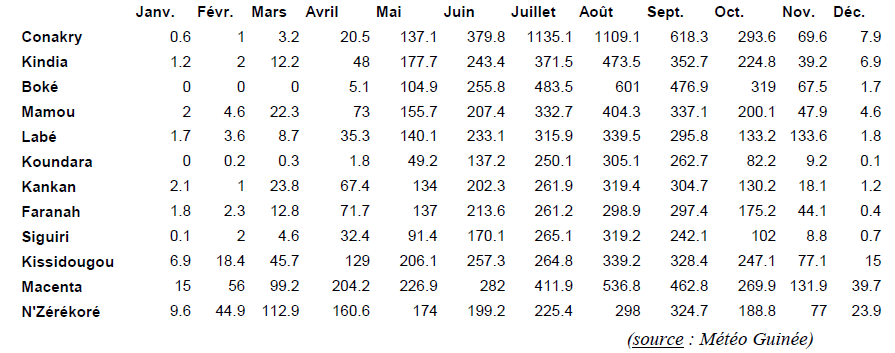
tab. 2 - Précipitations moyennes mensuelles de 12 villes guinéennes (DUMOLARD 2005, tab. 2.3) => matrice d'information spatio-chronologique
Objectif principal : former des groupes d'individus
- Les classifications ascendantes hiérarchiques (CAH)
Une des techniques les plus utilisées en géographie.
Permet :
- d'effectuer des typologies emboîtées ;
puis
- des cartographies.
- Les classifications autour de centres mobiles, type nuées dynamiques
- Méthodes utilisées sur de très grosses populations
- Permet de rechercher le nombre de classes optimales le plus stable (robuste)
repose sur un grand nombre d'itérations
- Les classifications à limites mobiles ou floues
- Quand les classes obtenues :
- ne sont pas disjointes ;
- reposent sur des probabilités d'appartenance...
Ces deux dernières ne seront pas abordées ici.
Les analyses factorielles et les techniques de classification sont complémentaires.
On sera donc amené à les utiliser conjointement.
Elles permettent :
- de tester de nombreuses hypothèses,
mais n'ont aucun pouvoir explicatif !
- d'extraire successivement des résumés unidimensionnels indépendants et hiérarchisés dont l'importance informative (variance) est dégressive.
Ce sont des techniques exploratoires pour réduire la complexité initiale du tableau d'information.
- Quelles sont les étapes d'une analyse avec SPAD ?
Pour partir à la découverte des principes généraux de SPAD 9 :
- Lancez SPAD depuis : Démarrer + Tous les programmes + SPAD 9
Une fois SPAD démarré :
- Cliquez sur le "?" dans la barre des menus + Sommaire de l'aide
- Dans le menu de gauche de la fenêtre d'aide, rendez actif :
SPAD Version 9\Présentation générale
- Dans le menu de droite, cliquez sur :
Le projet SPAD \Un exemple
Laissez vous guider !
Anciennement appelées Filières, la nouvelle interface graphique, qui chaîne des modules, est maintenant appelée Diagramme !
- La procédure de traitements, bien que plus graphique, reste la même.
- Il faut d'abord Importer les données :
- le plus simple étant de générer, à partir d'EXCEL :
- un fichier texte ASCII en alphanumérique* avec les :
- individus* en lignes
- variables* en colonnes
- un fichier SPSS (*.sav)
- un fichier Access (*.mdb)...
Mais les tables SAS (format XPORT) ne semblent plus directement importables !
- Puis mouliner les données importées à l'aide d'une succession de Modules, qu'il faut paramétrer
- Parmi ces modules certains sont des outils, Onglet Data Management, permettant de créer de nouvelles variables par :
- recodage => mise en classes, croisement, opération, ...
- quantile* => pour mettre en classes d'effectifs égaux* des données continues*
- redressement* => pour créer et conserver une variable poids par ajustement à des distributions*
- D'autres permettent des traitements multivariés comme les :
- Analyses factorielles (ACP, AFC, ACM...)
- Classifications - typologies (CAH...)
Si l'interface des diagrammes a changé par rapport à celui des filières (version SPAD antérieures à la V. 7)
en revanche, dans les méthodes l'utilisateur retrouve un paysage familier !
- Paramétrage des méthodes
Après avoir fait glisser de la fenêtre Méthode à la fenêtre Diagramme l'icône d'une méthode
- Reliez-là à la base de données
- Faites un clique droit dessus
- Choisissez Paramétrer (ou sélection de la méthode et F4)
ou double clique sur l'icône de la méthode
- effectuer les choix demandés dans la boîte de dialogue
- cliquer sur OK
Dans la fenêtre Exécutions, la méthode s'exécute !
- Consultation des résultats
En double cliquant sur l'icône listage, EXCEL ou sur l'icône écran
- Le tableau EXCEL est-il compatible avec SPAD ?
Exemple n°1 : Tableau 2.1 - Dix mesures relatives à la qualité de la vie dans 18 grandes métropoles américaines (Sources : M.V. JONES and M.J. FLEX, The quality of life in Washington D.C., The Urban Institute, Washington D.C, 1970. in SANDERS 1989, p. 57)
Ce fichier est au format EXCEL 5.0 et "pèse" 97 Ko.
Téléchargement du script bivar_villeUS_v2.R
Exemple n°2 : AMAT (J.-P.), GODARD (V.), HOTYAT (M.) - 2003 - Milieu, gestion, histoire et scénarios de reconstitution dans les sylvosystèmes touchés par les tempêtes de décembre 1999, GIP-ECOFOR, Min. agriculture, 115 p.
Ce fichier est au format texte tabulé et "pèse" 5 Ko.
Exemple n°3 : Tableau 4.1 - La structure pastorale éthiopienne par Awrajas (en nombre de têtes), [Sources : EASTMAN (J.R.) - 1997 - 10. Database Workshop. in : IDRISI for Windows. Tutorial Exercises. Version 2.0. Worcester (MA, USA), Clark University, pp. 69-79 et traduction française GODARD, 2003]
Ce fichier est au format EXCEL (.xls) et "pèse" 51 Ko.
Ce tableau est le support d'un exercice détaillé sur le fiche guide 1.8 du cours de SIG.
L'import des données se fait comme expliqué sur la fiche mémo mem04dea.htm du cours de Master 2.
Exemple n°4 : Pauvreté à Revere (Massachussetts, USA)
Ce fichier est au format EXCEL (.xls) et "pèse" 46 Ko.
Exemple n°5 : Le premier tours des élections législatives de 2012 par département
Accéder aux données d'un certain nombre d'élections (data.gouv.fr)
Pour décrypter les sigles des différents partis : Wikipédia
Exemple n°6 : Quelques équipements de santé en 2012 par département
Les données portent sur : les établissement qui ont des urgences (urg) ; des maternités (mat) ; des pharmacies (pha) ; et des laboratoires d'analyse (lab) pour 100 000 habitants.
Sous EXCEL :
- Sélectionner les données utiles dans la feuille "brut"
de A2 à K21
Pas de blancs ni de caractères spéciaux dans les intitulés de variables
- Les coller par Collage spécial du menu Edition
en A1 de la feuille "txt"
- Faire un Enregistrer sous du menu Fichier
Le type de fichier doit être en :
Texte tabulé (*.txt)
L'enregistrer dans votre répertoire en :
D:\Users\geographie\Votre_Nom\ADD\villesUS\ta1fm02d.txt
- Comment passer d'un tableau EXCEL à une base SPAD ?
- Lancer SPAD
- Cocher "Créer un nouveau projet"
- Sélectionner le répertoire :
D:\Users\geographie\Votre_Nom\ADD\villesUS\
- Cliquer sur OK.
- Sélectionner dans la fenêtre "Méthodes"
Imports / Exports de données\Imports\Fichier Texte Délimité
- Le faire glisser dans la fenêtre "Diagramme"
- Double-cliquer sur son icône pour la paramétrer
"Fichier texte direct" étant coché
- Sélectionner le fichier texte des villes US :
D:\Users\geographie\Votre_Nom\ADD\villesUS\ta1fm02d.txt
- Cliquer sur OK.
- Laisser les paramètres par défaut.
- Sélectionner l'onglet "Métadonnées" pour définir le typage des variables, c'est là que l'on peut :
- choisir ou non d'importer une variable (Impor...) ;
- changer son nom pour les traitements à venir (Nouveau nom) ;
- modifier les caractéristiques de son stockage qui peut être : Autre, Chaîne, Réel, Entier, Date (Cliquer sur Aide pour en savoir plus) ;
- modifier le "Rôle" de la variable villes de :
Nominal => Identifiant
- pour Exécuter l'importation cliquer sur OK.
- Pour vérifier que l'exécution s'est bien déroulée, aller voir la fenêtre "Exécutions" et ses différents onglets.
- Insertion d'une première méthode
- Sélectionner dans la fenêtre "Méthodes"
Statistiques descriptives\ Caractérisation d'une variable quantitative
- Le faire glisser dans la fenêtre "Diagramme" à côté de la base de données ta1fm02d
- tirer une flèche bleue entre la base de données et la méthode statistique
ta1fm02d => Description Var Quanti
- Double-cliquer sur son icône pour la paramétrer (ou la sélectionner + F4)
pour choisir les variables à caractériser et caractérisantes
Onglet Variables
- Sélection des variables : continues à caractériser
=> toutes
- Sélection des variables : continues caractérisantes
=> toutes
- Insertion d'une deuxième méthode
- Sélectionner dans la fenêtre "Méthodes"
Statistiques descriptives\Tris-à-plat, moyennes, histogrammes...
ou faire glisser l'icône de "Tris-à-plat, histogrammes" sur l'icône de la méthode précédente
Attention "Tri-à-plat" est réservée aux variables qualitatives* (nominales*)
- ou tirer une flèche bleue entre la base de données et la méthode statistique
Description Var Quanti => Stats
- Double-cliquer sur son icône pour la paramétrer (ou la sélectionner + F4)
Onglet Histogrammes - Discrétisation
Pour choisir les Variables
- Sélection des variables : Pour histogrammes/Statistiques sommaires
("Pour discrétisation" ne fonctionne pas sur des variables continues)
- Variables sélectionnées :
- => toutes
- Insertion d'une troisième méthode
- Sélectionner dans la fenêtre "Méthodes"
Statistiques descriptives\Analyse bivariée
ou faire glisser l'icône de "Analyse bivariée" sur l'icône de la méthode
- ou tirer une flèche bleue entre la base de données et la méthode statistique
Stats => Analyse bivariée
- Double-cliquer sur son icône pour la paramétrer (ou la sélectionner + F4)
Onglet Variables
Pour choisir les Variables AXES
- Variable 1 : UNEM
- Variable 2 : SUIC
Pour choisir les Variables de description
- Continues illustratives
- => toutes
- Pour vérifier que l'exécution s'est bien déroulée, aller voir la fenêtre "Exécutions" et ses différents onglets.
Dans la fenêtre "Exécutions"
- Cliquer sur la galerie de graphiques
Pour choisir les Variables
- => toutes
Pour choisir la Galerie
- Lignes : 10
- Colonnes : 10
(il y a 10 variables, le pavage graphique fera 10*10 = 100 histogrammes !)
Agrandir la fenêtre si nécessaire !
- Information sur les individus
- Déplacez le pointeur sur lui !
- Dans la barre d'état
- le nom à gauche
- la valeur pour les deux variables à droite
- Information sur une cellule
- Double clique sur la cellule
On obtient par variable :
- moyenne
- écart-type
- nombre de valeurs manquantes
- coeff. de corrélation (r)
- coeff. de régression (a)
- ordonnée à l'origine (b)
du "y=ax+b" qui décrit la droite de régression
(on peut se rafraîchir les notions sur la régression linéaire avec le cours de Claude GRASLAND ici)
- Le balayage
Pour désigner des points que l'on veut localiser sur tous les graphiques
- Sélectionner le bouton balayage
(ou Menu Outils + Balayage)
- Sélectionner sur un graphique les points (villes) :
- Los Angeles
- San Francisco
(déjà isolés sur la variable SUICide)
Un clique bouton droit dans une zone balayée indique les individus présents
- Modifier la configuration du balayage
Menu Outils + Configuration du balayage
La fenêtre Couleur et habillage pour le balayage apparaît.
Modifier les paramètres
- Les histogrammes
Pour obtenir les "histogrammes" des variables de la galerie
- Sélectionner le bouton histogrammes
(ou Menu Outils + Histogramme)
La fenêtre Configuration de l'histogramme apparaît.
- Déterminer le nombre de barres
- Combien faut-il de barres ?
Si vous ne savez pas comment le déterminer, cliquez là !
- Sélectionner le bouton Histogrammes et courbes de densité normale
- Sélectionner le bouton Valeurs
Cliquer sur OK
- Comment interpréter cela ?
- Coeff. de symétrie (skewness dans Excel, SPSS...) : mesure la symétrie de la courbe par rapport à la loi normale centrée réduite (Coeff. de symétrie = 0) :
- Coeff. de symétrie < 0
la courbe est tronquée à droite et décalée à gauche
- Coeff. de symétrie > 0
la courbe est tronquée à gauche et décalée à droite
- Coeff. d'aplatissement (kurtosis dans Excel, SPSS...) : mesure l'aplatissement de la courbe par rapport à la loi normale centrée réduite (Coeff. d'aplatissement = 3) :
- Coeff. d'aplatissement < 3 (<0 dans Excel car kurtosis normalisé, cf. le kurtosis de Wikipédia)
la courbe est plus aplatie que la loi normale centrée réduite
- Coeff. d'aplatissement > 3 (>0 dans Excel car kurtosis normalisé, cf. le kurtosis de Wikipédia)
la courbe est plus pointue que la loi normale centrée réduite
=> fait référence aux tests statistiques ;
=> est exprimée en nombre d'écart-type d'une loi normale (Morineau & Aluja-Banet 2000, p.51)
si :
- La valeur-test > 2
Cela signifie qu'on s'éloigne d'une loi normale du nombre de valeur-tests indiqué
=> ici plus de 2
- La valeur-test < 2
Cela signifie qu'on se rapproche d'une loi normale du nombre de valeur-tests indiqué
Pour en savoir plus sur les tests statistiques, cliquez ici
En résumé, ici, on utilisera la moyenne et l'écart-type pour décrire une variable quand VT < 2
- Qu'en est-il de la distribution des SUICides ?
- Et pour les autres, s'éloignent-elles significativement de la loi centrée réduite ?
- Sont-elles pour autant proches de cette loi (cf. coef. sym. et applat.) ?
- La régression linéaire
Pour afficher la droite de régression linéaire sur toutes les cellules de la galerie de graphiques.
- Sélectionner le bouton Régression linéaire
(ou Menu Outils + Régression linéaire)
(là encore, on peut se rafraîchir "les notions" sur la régression linéaire avec le cours de Claude GRASLAND ici)
- Simple clique sur les rapports
- Qu'est-ce que le coefficient de variation* (CV) ?
- Qu'est-ce que le coefficient de corrélation* ?
(là encore, on peut se rafraîchir "les notions" sur la corrélation linéaire avec le cours de Claude GRASLAND ici)
- Simple clique sur le graphe
Faire :
- Graphique + Nouveau (Ctrl + N)
- Sélectionner toutes les options
Puis à titre d'exercice
- mettre un nom aux différentes villes
- Menu Sélection + De tous les points
- Menu Habillage + Ecrire les libellés
- relier les villes "géographiquement" proches
- Menu Dessin + Segments
- Le chômage et le suicide sont-ils liés (corrélés) ?
- Y a-t-il une spatialisation du suicide ou du chômage ?
- Les chômeurs se suicident-ils beaucoup ?
Notion d'erreur écologique* pour en savoir plus sur l'EE cliquer ici
|
Communiquez-moi sur la plateforme Moodle, à la rubrique "Questions de cours", les réponses aux questions suivantes :
Question n°1.1. Parmi les expressions suivantes, y en a-t-il une ou plusieurs qui ne caractérise(nt) pas le coefficient de corrélation linéaire :
Question n°1.2. Parmi les expressions suivantes, y en a-t-il une ou plusieurs qui ne caractérise(nt) pas la normalité d'une distribution :
Question n°1.3. Parmi les expressions suivantes, y en a-t-il une ou plusieurs qui ne caractérise(nt) pas un test statistique :
|
NB : les mots suivis de "*" font partie du vocabulaire statistique, donc leur définition doit être connue. Faites-vous un glossaire.