Vincent GODARD
Département de Géographie
Université de Paris 8
V.2.9- Dernière mise à jour : 29/11/2022
Fiche Mémo n°2 d'analyse de données pour le
Master 2 :
L'analyse en composantes principales (ACP)
Note : ce cours d'analyse de données multivariées doit beaucoup à
l'ouvrage de Lena Sanders,
maintenant épuisé (sauf en bibliothèques, mais téléchargeable ici). Qu'elle en soit ici remerciée pour sa
contribution (involontaire ;-) !).
1. Principes
1.1. Contexte
- caractères quantitatifs
Qui peuvent être exprimés simultanément :
- dans la même unité (% ou surfaces, ...) ;
- dans différentes unités (% et surfaces, ...) ;
Regroupés dans un tableau
de mesures*
Le tableau de mesures est constitué de :
- n individus statistiques ;
qui peuvent être des unités
spatiales (tableau
de données = tableau
d'information géographique)
- p variables quantitatives.
1.2. Objectifs
Comme les autres analyses factorielles, l'ACP va surtout s'intéresser à l'étude des colonnes
(variables) du tableau d'information pour confronter les différentes distributions et permettre :
- de découvrir des
irrégularités dans ces distributions ;
- d'analyser des
interrelations entre les variables ;
- de mettre en évidence des
combinaisons plus ou moins systématiques entre les
variables ;
En bref, de dégager les
composantes sous-jacentes qui structurent l'espace géographique étudié.
Cela passe par une simplification de
l'information d'origine
1.3. Les différentes phases d'une ACP
Les calculs, qui relèvent de la distance euclidienne*,
tiennent en trois phases :
- Constitution d'une matrice
d'information (spatiale
ou non)
- Les "n"
individus doivent former un ensemble
cohérent
pas d'individus exceptionnels
- Les "p"
variables peuvent être hétérogènes
- en valeurs absolues ;
- en valeurs relatives ;
- dans des unités de
mesures différentes, ...
- Transformation des données
d'origine
- par simple centrage* des données
mais, il faut que toutes les données aient la même unité
la matrice d'information devient :
=> une matrice des covariances* entre variables
- par centrage
et
réduction* des données (standardisation*)
la matrice d'information devient :
=> une
matrice des corrélations* entre
variables
- Qu'est-ce que le centrage et la
réduction ?
A partir d'un exemple.
Exemple n°1 : Tableau 2.1a - Dix mesures
relatives à la qualité de la vie dans 18 grandes métropoles américaines
(Sources : M.V. JONES and M.J. FLEX, The quality of life in Washington
D.C., The Urban Institute, Washington D.C, 1970. in SANDERS 1989,
p. 57)
Téléchargement
du
fichier de données
Ce fichier est au format EXCEL 2016 et "pèse"
10 Ko.
En général, on réalise des ACP
normée*. Cela signifie que :
- les variables sont standardisées ;
- la projection utilisée est orthogonale ;
- le critère d'ajustement est celui des moindres
carrés*.
Alors, la matrice
de relations (dite matrice d'inertie*), ex
matrice d'information, est devenue :
- une matrice
des
corrélations* entre variables
- C'est une matrice carrée d'ordre "p" ("p"
lignes sur "p"
colonnes)
avec une diagonale qui vaut 1
- Que faire lorsque les données ne
sont pas distribuées normalement ?
La littérature propose un autre type de
transformation qui consiste à essayer de "normaliser" la distribution pour qu'elle se rapproche d'une
distribution normale :
ftp://ftp.unice.fr/users/francour/Cours_Stat_6.pdf
http://www.fao.org/docrep/003/x6831f/X6831f08.htm
http://statistiques.forumpro.fr/t3283-transformation-de-donnees-pour-avoir-une-loi-normale
http://biol09.biol.umontreal.ca/bio2042/Marie/laius_4.pdf
http://biol09.biol.umontreal.ca/bio2042/Transf_donn.pdf
Un développement avec graphique explicatif est
proposé ici (il s'appuie sur un passage du cours de cartographie de
L2) : Transformations de variables.
Il précise l'effet sur une
distribution lorsque celle-ci comporte une asymétrie droite ou
gauche, en fonction des fonctions de transformation (logarithme ou
puissance avec un exposant <1 ou >1 par exemple).
Faut-il encore s'être
assuré de la non normalité des variables !
Deux coefficients servent
de "juges de paix" pour évaluer cette non normalité :
- le coefficient d'asymétrie de Fisher
(aussi appelé Skewness) ;
- le coefficient d'aplatissement de
Pearson (aussi appelé Kurtosis).
Cette transformation n'est
pas systématique ou obligatoire, elle dépend des écoles !
- Dans leur paquet
(package) Factominer
sur l'ACP, François Husson, Julie Josse,
Sébastien Lê et J. Mazet (qui font référence !) n'évoquent pas de
transformations des données, ni le problème de la non normalité de
la distribution !
- Dans son blog R-atique, Lise Vaudor, qui reprend l'exemple
des résultats pour différentes épreuves du Décathlon développé
ci-dessus par François Husson et al., n'évoque pas non plus
le contrôle de la normalité des distributions avant de réaliser une
ACP
!
Donc
sentez vous libre. Expérimentez !
- Recherche
des axes factoriels*
Cette recherche se fait sur la matrice d'inertie
- Chaque axe factoriel est défini par
un vecteur dit
vecteur propre* (eigenvectors)
Ils définissent les différentes directions du nuage
d'information
- La part d'information prise par chaque vecteur propre est appelée
valeur propre* (eigenvalues)
Elle définie la hiérarchie de l'axe factoriel.
Un exemple des combinaisons linéaires caractéristique de
l'ACP est proposé dans le cours de télédétection, accessible ici, et de calcul
des équations de transformation à partir des vecteurs propres est donné
ici.
1.4. Les résultats d'une ACP
Ils sont de quatre types pour chaque
axe factoriel :
- part d'information totale
prise en compte par l'axe ;
- valeur propre
= part de variance (d'information) du nuage prise en compte par l'axe
- généralement exprimée
en pourcentage
on parle indifféremment de pourcentages :
- d'inertie
- d'information
- de variance
Les trois résultats suivants sont
différents selon que l'on s'intéresse aux variables ou aux individus.
1.4.1. Les résultats sur les
sorties relatives aux variables
Résultats en général symétriques à ceux
des individus
- Les coordonnées (ou saturation,
loadings) des variables sur les
axes factoriels :
- sont le coefficient de corrélation entre la variable
et cet axe ;
- varient entre +1 et -1 (+ 1 000 et - 1 000 selon les
logiciels) ;
- peuvent être toutes du même côté (axe
d'intensité).
- Les contributions (CTR) des variables aux
axes factoriels :
- mesurent le rôle relatif de
chaque variable dans la construction (la
caractérisation) de l'axe factoriel
Elles permettent de repérer quelles sont les
variables les plus contributives par axe
- la somme des contributions vaut 1
- généralement exprimée en pour cent ou pour mille
Elles permettent :
- d'identifier les variables qui définissent le
mieux les axes ;
les plus contributives !
- d'isoler les variables qui ont un comportement exceptionnel (ou aberrant).
- La
qualité
(QLT ou Cos2)
de représentation d'une variable sur un axe factoriel :
- est donnée par le carré
de sa coordonnée sur cet axe ;
- mesure la part de la variable expliquée par
l'axe ;
Additionner le carré de
sa coordonnée pour deux axes, c'est obtenir la part de la variable expliquée sur ce plan factoriel.
1.4.2. Les résultats sur les sorties relatives aux individus
- Les coordonnées* (ou scores)
des individus sur
les axes factoriels :
- permettent de situer les individus le
long des axes
- peuvent être positifs ou négatifs (marquent
des oppositions).
- Les contributions* (CTR) des individus aux
axes factoriels :
- indiquent comment les individus contribuent à la formation (la caractérisation) de l'axe
factoriel
- la somme des contributions vaut 1
- généralement exprimée en pour cent ou pour mille
Elles permettent :
- d'identifier les individus qui définissent le
mieux les axes
- d'isoler les individus qui ont un comportement exceptionnel (ou aberrant).
Ceux qui concentrent la moitié ou presque des
contributions
- La
qualité*
(QLT ou Cos2)
de représentation des individus sur les axes factoriels :
- permet de caractériser
les individus par les axes
- mesure la part de l'écartement
d'un
individus
au centre de gravité prise en compte par un axe
QLT = cos2 (de l'angle entre le vecteur-individu et l'axe)
cos2 (0°) = 1
=> individu sur l'axe
(description parfaite de l'individu par l'axe)
cos2 (90°) = 0
=> individu perpendiculaire à l'axe
(description nulle de l'individu par l'axe)
- généralement exprimée en pour cent ou pour mille
Dans SPAD entre 0 et 1 !
Remarques :
- Les résultats ne sont
affirmés que pour les valeurs ayant les plus fortes coordonnées
Plus on est proche du barycentre :
- plus les variables sont étrangères à
la définition de l'axe ;
- moins les points sont concernés par
l'opposition des variables ;
ou
- moins la qualité de leur
représentation est bonne (ils sont loin du
facteur)
- Scores
et saturations ne
sont pas exprimés dans les mêmes unités de mesure
Cependant les vecteurs-individus
et vecteurs-variables ont la même direction
Par convention, on peut superposer
sur
les nuages de points, tracées sur les
cartes factorielles, des
flèches représentant chaque vecteur-variable.
Chaque flèche d'une longueur quelconque passe par le
barycentre* (0;0) et les coordonnées du vecteur-variable.
2. Analyse d'un 1er exemple
Exemple n°1 : Tableau 2.1a - Dix mesures relatives à la
qualité de la vie dans 18 grandes métropoles américaines (Sources
: M.V. JONES and M.J. FLEX, The quality of life in Washington D.C.,
The Urban Institute, Washington D.C, 1970. in SANDERS 1989, p. 57)
Téléchargement
du
fichier de données
Ce fichier est au format EXCEL 5.0 et "pèse" 97 Ko.
Téléchargement du script ACP_villeUS_v3.R
- Affichage du résumé de ce script généré en R Markdown ACP_villeUS_v5.Rmd (en html)
- Affichage du résumé de ce script généré en R Markdown ACP_villeUS_v5_vg.Rmd (en .Rmd)
- Affichage de l'aide à l'analyse Investigate(res.villeUS.pca) inclus dans le R
Markdown ci-dessus (générée pour la v4).
2.1. Procédure
- Si
ce n'est pas fait, pour importer les données et créer
un nouveau projet avec un nouveau diagramme,
se reporter à la fiche mémo mem01mas.htm.
Dans la fenêtre Diagramme :
- Après l'import du fichier texte délimité
depuis la fenêtre Méthodes, insérer une
première méthode
- Clic droit sur l'icône
de "ta1fm02d"
puis Ajouter méthode
(ou Insérer)
- Choisir : Analyse
factorielle / Composantes principales (ACP)
Valider avec OK
- Clic droit sur l'icône
de la méthode + Paramètres ... (ou F4)
Onglet Variables
- Sélection des variables : Continues actives
=> toutes
Onglet Individus
- Choix des individus
=> tous
Onglet Pondération
=> Uniforme
Onglet Paramètres
- Paramètres de fonctionnement :
Analyse
normée
Coordonnées conservées
toutes
- Paramètres d'édition :
Matrice permutée selon F1 Non
Coordonnées éditées
toutes
Résultats pour les individus tous
Nombre de décimales
2
- Fichier pour application tableur : Oui
- Cliquer sur Option
Résultats pour les individus Oui
- Valider avec OK
- Insertion d'une deuxième méthode
Toujours dans la fenêtre Diagramme :
- Clic droit sur l'icône
de "ACP" puis Ajouter méthode (ou Insérer)
- Choisir : Analyse
factorielle / Description des facteurs (DEFAC)
Valider avec OK
- Clic droit sur l'icône
de la méthode + Paramètres ... (ou F4)
Onglet Commande
de
description
- Liste des axes à décrire : 1-6
- Avec les éléments :
Variables continues
Actives seules
Individus
Actifs seuls
- Fichier pour application tableur : Oui
- Cliquer sur Option
Résultats pour les individus Oui
- Valider avec OK
2.2. Analyse
2.2.1. Analyse des valeurs de la matrice des corrélations
- Où trouver la matrice des
corrélations ?
- Simple
clic sur le plan du rapport
- Listage de l'analyse en composantes principales
- Recherche de la matrice des corrélations
- Quelles sont les variables
corrélées entre elles ?
- Quelle est l'intensité de la
liaison ?
- Qu'est-ce que cela signifie ?
tab. 1 - Matrice des corrélations
|
|
INCO
|
UNEM
|
LOWI
|
HCOS
|
MENT
|
INFM
|
SUIC
|
POLL
|
ROBB
|
TRAF
|
|
INCO
|
1
|
|
|
|
|
|
|
|
|
|
|
UNEM
|
0.11
|
1
|
|
|
|
|
|
|
|
|
|
LOWI
|
0.11
|
0.35
|
1
|
|
|
|
|
|
|
|
|
HCOS
|
-0.05
|
-0.12
|
-0.48
|
1
|
|
|
|
|
|
|
|
MENT
|
0.10
|
-0.18
|
-0.11
|
-0.06
|
1
|
|
|
|
|
|
|
INFM
|
-0.03
|
-0.15
|
0.07
|
-0.31
|
0.42
|
1
|
|
|
|
|
|
SUIC
|
0.45
|
0.64
|
0.49
|
-0.04
|
-0.18
|
-0.43
|
1
|
|
|
|
|
POLL
|
-0.03
|
0.13
|
-0.35
|
0.37
|
0.36
|
0.25
|
-0.16
|
1
|
|
|
|
ROBB
|
0.45
|
0.26
|
-0.07
|
0.05
|
0.56
|
0.15
|
0.19
|
0.33
|
1
|
|
|
TRAF
|
0.37
|
0.38
|
0.51
|
-0.51
|
-0.26
|
0.01
|
0.62
|
-0.54
|
0.05
|
1
|
- Il est parfois
utile de faire un graphique pour voir les liens :
- opposition positif / négatif ;
- épaisseur variable du trait en fonction de
l'intensité:
- trait épais quand
Coef. de cor. > 0,8
- trait fin quand
0,6 < Coef. de cor. < 0,8
- pas de liaisons dessinées en deçà (les limites sont
données à titre d'exemple, les adapter au cas étudié)
- Il est également utile
d'analyser la matrice des valeurs tests
Surtout pour les grands tableaux
tab. 2 - Matrice des valeurs tests
|
|
INCO
|
UNEM
|
LOWI
|
HCOS
|
MENT
|
INFM
|
SUIC
|
POLL
|
ROBB
|
TRAF
|
|
INCO
|
99.99
|
|
|
|
|
|
|
|
|
|
|
UNEM
|
0.47
|
99.99
|
|
|
|
|
|
|
|
|
|
LOWI
|
0.47
|
1.57
|
99.99
|
|
|
|
|
|
|
|
|
HCOS
|
-0.22
|
-0.51
|
-2.24
|
99.99
|
|
|
|
|
|
|
|
MENT
|
0.44
|
-0.79
|
-0.46
|
-0.24
|
99.99
|
|
|
|
|
|
|
INFM
|
-0.12
|
-0.66
|
0.29
|
-1.36
|
1.91
|
99.99
|
|
|
|
|
|
SUIC
|
2.08
|
3.20
|
2.29
|
-0.17
|
-0.78
|
-1.94
|
99.99
|
|
|
|
|
POLL
|
-0.13
|
0.55
|
-1.57
|
1.63
|
1.58
|
1.09
|
-0.68
|
99.99
|
|
|
|
ROBB
|
2.05
|
1.13
|
-0.30
|
0.22
|
2.67
|
0.64
|
0.82
|
1.45
|
99.99
|
|
|
TRAF
|
1.63
|
1.68
|
2.41
|
-2.41
|
-1.12
|
0.04
|
3.10
|
-2.56
|
0.21
|
99.99
|
Elle permet :
- de tester la
significativité des coefficients de corrélation
C'est un test statistique exprimé en nombre
d'écart-types d'une loi normale (cf. aide de SPAD)
En clair :
- si la valeur lue est supérieure à 2, le coeff.
est significatif avec un risque d'erreur de 5% ;
- plus la v-test est grande (en valeur absolue)
- plus la liaison entre variables est
significative ;
- moins le hasard a de chance d'être
responsable de celle-ci.
Pour plus de détails sur les tests, voir la fiche
mémo les introduisant (cf. Annexe
n°2 du cours d'enquête)
- de classer
par ordre d'importance les liens entre les variables
- Quelles corrélations entre
variables retenez-vous au seuil de 0,05 ?
Reproduire la matrice des corrélations dans EXCEL en
coloriant les cellules qui satisfont aux conditions de la matrice
des valeurs tests.
2.2.2. Analyse des valeurs propres
Pour savoir où trouver l'information
- Où trouver les valeurs propres ?
=> Copri 4
- Double clic sur le plan du rapport
- Listage de l'analyse en composantes principales
- Double clic sur Valeurs propres
On obtient cela :
fig. 2 - Matrice des valeurs propres

- La colonne VALEUR PROPRE indique l'inertie le long de
chaque axe factoriel.
La somme est l'inertie globale du nuage et vaut 10
(le nombre de variables actives dans une ACP normée).
- La colonne POURCENT. exprime le pourcentage d'inertie
porté par chaque axe.
- La colonne POURCENT. CUMULE donne le pourcentage
cumulé d'inertie.
- Quelle est la répartition de la
variance sur les facteurs ?
- 31 % de l'information du nuage de points est
résumé par le premier axe !
- 80 % de l'information est sur les 4 premiers axes
!
- Combien d'axes faut-il retenir ?
- il n'y a pas de réponses automatiques !
- si toutes les variables sont très corrélées, peu
d'axes suffiront !
- les axes discriminants ne sont pas forcément les
premiers !
2.2.3. Analyse des axes
Objectif : rechercher les
associations de variables
Pour caractériser les facteurs
- Où trouver les informations sur
les axes ?
- Analyse du plan du rapport :
Simple clic sur le plan du rapport
- Listage de l'analyse en composantes principales
- Double clic sur Coordonnées
des variables de 1 à 5
- Quelles sont les variables qui
qualifient chaque axe ?
- Où sont les Contributions et
qualités ?
=> Copri 6
tab. 3 - Coordonnées, contributions et
qualités des variables sur les cinq 1er
facteurs
|
VARIABLES
|
COORDONNÉES
|
CORRÉLATIONS VARIABLE-FACTEUR
|
ANCIENS AXES UNITAIRES
|
|
IDEN
|
1
|
2
|
3
|
4
|
5
|
1
|
2
|
3
|
4
|
5
|
1
|
2
|
3
|
4
|
5
|
|
INCO
|
-0.40
|
0.54
|
-0.14
|
0.58
|
-0.30
|
-0.40
|
0.54
|
-0.14
|
0.58
|
-0.30
|
-0.22
|
0.37
|
-0.11
|
0.57
|
-0.39
|
|
UNEM
|
-0.58
|
0.31
|
-0.33
|
-0.59
|
-0.09
|
-0.58
|
0.31
|
-0.33
|
-0.59
|
-0.09
|
-0.33
|
0.21
|
-0.25
|
-0.58
|
-0.11
|
|
LOWI
|
-0.72
|
0.00
|
0.32
|
-0.27
|
0.25
|
-0.72
|
0.00
|
0.32
|
-0.27
|
0.25
|
-0.41
|
0.00
|
0.24
|
-0.26
|
0.33
|
|
HCOS
|
0.48
|
0.00
|
-0.74
|
0.08
|
-0.02
|
0.48
|
0.00
|
-0.74
|
0.08
|
-0.02
|
0.27
|
0.00
|
-0.56
|
0.08
|
-0.03
|
|
MENT
|
0.36
|
0.70
|
0.33
|
0.08
|
0.43
|
0.36
|
0.70
|
0.33
|
0.08
|
0.43
|
0.21
|
0.48
|
0.25
|
0.08
|
0.56
|
|
INFM
|
0.25
|
0.36
|
0.74
|
-0.19
|
-0.37
|
0.25
|
0.36
|
0.74
|
-0.19
|
-0.37
|
0.14
|
0.25
|
0.56
|
-0.19
|
-0.48
|
|
SUIC
|
-0.81
|
0.24
|
-0.43
|
-0.04
|
0.10
|
-0.81
|
0.24
|
-0.43
|
-0.04
|
0.10
|
-0.46
|
0.16
|
-0.33
|
-0.04
|
0.13
|
|
POLL
|
0.54
|
0.53
|
-0.26
|
-0.43
|
-0.23
|
0.54
|
0.53
|
-0.26
|
-0.43
|
-0.23
|
0.30
|
0.37
|
-0.20
|
-0.43
|
-0.29
|
|
ROBB
|
-0.02
|
0.88
|
-0.10
|
0.13
|
0.13
|
-0.02
|
0.88
|
-0.10
|
0.13
|
0.13
|
-0.01
|
0.61
|
-0.07
|
0.13
|
0.17
|
|
TRAF
|
-0.87
|
0.04
|
0.21
|
0.14
|
-0.19
|
-0.87
|
0.04
|
0.21
|
0.14
|
-0.19
|
-0.49
|
0.02
|
0.16
|
0.14
|
-0.24
|
Interprétation :
- La colonne COORDONNÉES donne la projection des variables sur les 5 premiers axes factoriels.
On peut constater qu'elles sont toutes positives sur
l'axe 2.
- le nuage est décentré ;
- c'est un axe d'intensité (facteur de taille).
- La colonne CORRÉLATIONS
VARIABLE-FACTEUR permet d'apprécier la qualité du positionnement des variables sur les 5 premiers axes factoriels.
mais dans SPAD les CORRÉLATIONS
VARIABLE-FACTEUR ne sont pas élevées au carré, il faut le faire
dans Excel !
- En ACP normée, les Cos2
coïncident avec le carré des coordonnées des variables ;
- Quand la valeur d'un Cos2
est-elle élevée ?
Là non plus, la réponse n'est pas automatique,
Pour déterminer les variables bien représentés, il faut comparer les sommes des Cos2 plan par plan.
- sur le 1er plan, axe 1 et 2, INCO est mieux représentée que HCOS
INCO => 0,94 = | -0,40 + 0,54 |
mais plus logiquement : INCO => 0,44 = -0,402 + 0,542
HCOS => 0,48 = | 0,48 + 0,00 |
mais plus logiquement : HCOS => 0,23 = 0,482 + 0,002
- HCOS est mieux représenté sur l'axe 3 (-0,74).
La somme du Cos2 atteint 1 dans le meilleur des cas.
- La colonne CONTRIBUTION
donne la contribution des variables à l'inertie portée sur les 5 premiers axes factoriels.
- sert à détecter les variables qui contribuent le plus à la formation des axes ;
- la contribution est :
CTR = (ANCIENS AXES UNITAIRES)2
La somme des contributions est égale à 1 (ou 100 en
pourcentage).
Pour s'y retrouver, il vaut
mieux calculer les contributions et les qualités
sur le fichier tableur.
- double clic sur l'icône Excel de la filière ;
ou
- télécharger ce même fichier mais "préparé"
Exemple n°1 : Tableau 2.1b - Dix mesures relatives à la
qualité de la vie dans 18 grandes métropoles américaines (Sources
: M.V. JONES and M.J. FLEX, The quality of life in Washington D.C.,
The Urban Institute, Washington D.C, 1970. in SANDERS 1989, p. 57)
Téléchargement
du
fichier de résultats
Ce fichier est au format EXCEL 98 et "pèse" 55 Ko.
Voir les :
- Matrice des corrélations en COPRI-2 ;
- en rouge les corrélations > 50
%
- en bleu les corrélations < -
50 %
- Matrice des valeurs-tests en COPRI-3 ;
- en rouge les corrélations > 2
- en bleu les corrélations < -
2
- Valeurs propres en COPRI-4 ;
- Coordonnées, COS2 et CTR des variables en COPRI-6 ;
Complétez les tableaux !
- Coordonnées, COS2 et CTR des individus en COPRI-9 ;
Complétez les tableaux !
- Analyse graphique d'un plan factoriel :
Double clic sur le graphique
- Présélections pour un nouveau graphique : variables
continues actives
Valider par OK
- Menu Sélection
+ De tous les
points
- Menu Habillage
+ Ecrire les
libellés
On obtient cela :
fig. 3 - 1er plan factoriel
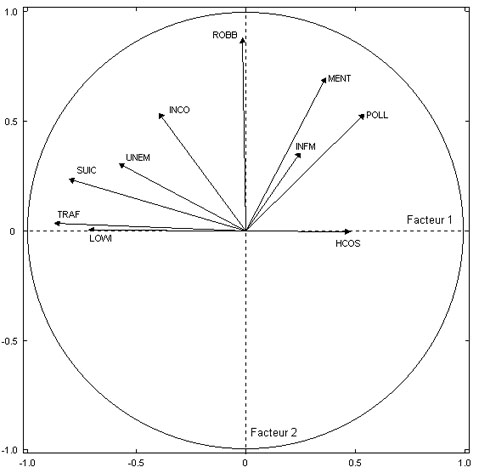
- Menu Habillage
+ Informations
sur les points
- Cliquer sur chaque pointe de flèches
- Noter les CTR, avec les
signes des coordonnées, dans une
fenêtre EXCEL !
C'est plus simple pour les individus !
Interprétation :
- 2 variables proches forment un angle aigu.
cela correspond à un Coefficient
de corrélation positif élevé (UNEM et
SUIC, r = +0,64) ;
- 2 variables avec un fort Coefficient de corrélation
négatif
sont diamétralement opposées (HCOS et LOWI, r =
-0,49) ;
- 2 variables indépendantes auront un Coefficient de
corrélation nul
et formeront un angle droit (TRAF et INFM, r =
+0,01) ;
- toutes les variables sont positives sur l'axe 2
le nuage des variables n'est pas centré !
2.2.4. Analyse des individus
Pour caractériser les groupes
d'individus
2.2.4.1. Par l'analyse du plan du rapport
- Simple clic sur le plan du rapport
- Listage de l'analyse en composantes principales
- Double clic sur Coordonnées,
contributions et cosinus
- Quels sont les individus qui
qualifient chaque axe ?
tab. 4 - Coordonnées, contributions et
qualités des individus sur les cinq 1er
facteurs
|
INDIVIDUS
|
|
|
COORDONNÉES
|
CONTRIBUTIONS
|
COSINUS CARRES
|
|
IDENTIFICATEUR
|
P.REL
|
DISTO
|
1
|
2
|
3
|
4
|
5
|
1
|
2
|
3
|
4
|
5
|
1
|
2
|
3
|
4
|
5
|
|
New York
|
5.56
|
14.76
|
2.27
|
2.56
|
-0.55
|
0.12
|
0.41
|
9.1
|
17.3
|
1.0
|
0.1
|
1.5
|
0.35
|
0.45
|
0.02
|
0.00
|
0.01
|
|
Los Angeles
|
5.56
|
17.27
|
-3.32
|
1.43
|
-1.61
|
-0.64
|
-0.20
|
19.5
|
5.4
|
8.3
|
2.2
|
0.4
|
0.64
|
0.12
|
0.15
|
0.02
|
0.00
|
|
Chicago
|
5.56
|
9.12
|
1.78
|
1.88
|
0.17
|
0.57
|
-1.07
|
5.6
|
9.3
|
0.1
|
1.8
|
10.6
|
0.35
|
0.39
|
0.00
|
0.04
|
0.13
|
|
Philadelphie
|
5.56
|
6.57
|
1.05
|
0.49
|
1.59
|
-0.98
|
-0.44
|
2.0
|
0.6
|
8.1
|
5.2
|
1.8
|
0.17
|
0.04
|
0.39
|
0.15
|
0.03
|
|
Détroit
|
5.56
|
5.37
|
0.07
|
1.45
|
-0.01
|
0.32
|
-1.11
|
0.0
|
5.5
|
0.0
|
0.6
|
11.3
|
0.00
|
0.39
|
0.00
|
0.02
|
0.23
|
|
Boston
|
5.56
|
12.64
|
2.51
|
-1.43
|
-1.84
|
0.54
|
0.10
|
11.2
|
5.4
|
10.8
|
1.6
|
0.1
|
0.50
|
0.16
|
0.27
|
0.02
|
0.00
|
|
San Francisco
|
5.56
|
24.04
|
-4.07
|
1.09
|
-2.24
|
0.30
|
0.53
|
29.3
|
3.1
|
16.1
|
0.5
|
2.6
|
0.69
|
0.05
|
0.21
|
0.00
|
0.01
|
|
Washington D.C.
|
5.56
|
10.47
|
1.78
|
1.32
|
0.00
|
1.44
|
1.36
|
5.6
|
4.6
|
0.0
|
11.1
|
17.2
|
0.30
|
0.17
|
0.00
|
0.20
|
0.18
|
|
Pittsburgh
|
5.56
|
6.06
|
-0.62
|
-0.49
|
0.20
|
-1.73
|
-0.57
|
0.7
|
0.6
|
0.1
|
16.2
|
3.0
|
0.06
|
0.04
|
0.01
|
0.50
|
0.05
|
|
St Louis
|
5.56
|
4.42
|
-0.47
|
-0.03
|
1.15
|
-0.58
|
-0.94
|
0.4
|
0.0
|
4.2
|
1.8
|
8.2
|
0.05
|
0.00
|
0.30
|
0.08
|
0.20
|
|
Cleveland
|
5.56
|
11.05
|
1.71
|
-1.02
|
-0.96
|
-1.92
|
1.07
|
5.2
|
2.7
|
2.9
|
19.9
|
10.6
|
0.27
|
0.09
|
0.08
|
0.34
|
0.10
|
|
Baltimore
|
5.56
|
5.83
|
0.16
|
1.53
|
1.31
|
-0.14
|
0.15
|
0.0
|
6.2
|
5.5
|
0.1
|
0.2
|
0.00
|
0.40
|
0.29
|
0.00
|
0.00
|
|
Houston
|
5.56
|
8.21
|
-1.65
|
-0.26
|
1.90
|
0.04
|
1.30
|
4.8
|
0.2
|
11.6
|
0.0
|
15.6
|
0.33
|
0.01
|
0.44
|
0.00
|
0.20
|
|
Minneapolis
|
5.56
|
8.67
|
-0.38
|
-1.93
|
-0.74
|
1.79
|
-0.57
|
0.3
|
9.7
|
1.8
|
17.3
|
3.0
|
0.02
|
0.43
|
0.06
|
0.37
|
0.04
|
|
Dallas
|
5.56
|
15.14
|
-1.78
|
-1.34
|
2.73
|
1.48
|
0.10
|
5.6
|
4.7
|
23.7
|
11.7
|
0.1
|
0.21
|
0.12
|
0.49
|
0.14
|
0.00
|
|
Cincinnati
|
5.56
|
5.58
|
0.23
|
-1.38
|
0.15
|
-0.36
|
0.95
|
0.1
|
5.0
|
0.1
|
0.7
|
8.4
|
0.01
|
0.34
|
0.00
|
0.02
|
0.16
|
|
Milwaukee
|
5.56
|
7.41
|
0.58
|
-1.98
|
-1.35
|
0.80
|
-0.67
|
0.6
|
10.3
|
5.8
|
3.4
|
4.1
|
0.05
|
0.53
|
0.25
|
0.09
|
0.06
|
|
Buffalo
|
5.56
|
7.37
|
0.13
|
-1.89
|
0.10
|
-1.05
|
-0.40
|
0.0
|
9.4
|
0.0
|
5.9
|
1.5
|
0.00
|
0.49
|
0.00
|
0.15
|
0.02
|
Interprétation :
- La colonne P. REL indique le poids donné à chaque individu (ville US) qui est dans ce cas uniforme (5,56 = 100 /
18).
- La colonne DISTO donne la distance au carré de chaque de chaque individu (ville US)
au centre de gravité du nuage. Cela permet de trouver les individus les plus
:
- moyens => les plus proches du centre de
gravité (St. Louis et Detroit) ;
- originaux => les plus loin du centre de
gravité (LA et SF).
C'est un critère d'originalité !
- La colonne COORDONNÉES donne la projection des individus (ville US) sur les 5 premiers axes factoriels.
- La colonne CONTRIBUTIONS (en %) donne la contribution des individus (ville US) à
l'inertie portée sur les 5 premiers
axes factoriels.
- sert à détecter les individus (ville US) qui contribuent le plus à la formation des
axes ;
- Quand la valeur d'une
contribution est-elle élevée ?
(quand elle est supérieure à la
contribution moyenne)
- si toutes les villes avaient la même
contribution, elle tournerait autour de 6% (5,6 = 100 / 18) ;
- sur le 1er axe SF (29,3) et LA (19,5) ont une contribution
supérieure à la moyenne ;
- sur le 2e axe NY (17,5) a une contribution supérieure à la
moyenne ;
Les individus (ville US) sont représentés sur la figure 4
proportionnellement à leur contribution.
La somme des contributions est égale à 100.
- La colonne COSINUS
CARRES permet d'apprécier la qualité du positionnement des individus (ville US) sur les 5 premiers axes factoriels.
- l'addition des Cos2, par plan factoriel, sert à détecter les individus (ville
US) qui sont les mieux représentés sur ce sous-espace défini par
ces 2 axes ;
- Quand la valeur d'un Cos2
est-elle élevée ?
Là non plus, la réponse n'est pas automatique,
Pour déterminer les individus (ville US) bien représentés, il faut comparer les
sommes des Cos2
plan par plan.
- sur le 1er plan, axe 1 et 2, NY est mieux représenté que
Pittsburgh
NY => 0,8 = 0,35 + 0,45
Pittsburgh => 0,10 = 0,04 + 0,06
- Pittsburgh est mieux représenté sur l'axe 4.
Les individus (ville US) sont représentés sur la figure 5
proportionnellement à leur qualité.
La somme du Cos2 atteint 1 dans le meilleur des cas.
2.2.4.2. Par l'analyse graphique des Contributions (CTR)
- Modification des Couleurs et symboles
- Double clic sur le graphique
- Présélections pour un nouveau graphique : individus
actifs
Valider par OK
- Menu Sélection
+ De tous les
points
- Menu Habillage
+ Ecrire les
libellés
- Menu Habillage
+ Couleurs et
symboles
Symboles = cercle
Couleur = rose
Taille proportionnelle = contributions
Valider par OK
- Paramétrage
de la proportionnalité
- Menu Dessin
+ Paramétrer la
proportionnalité
Taille minimale des symboles en pixels = 1
Taille maximale des symboles en pixels = 16
Ce paramétrage permet d'accentuer la
différence entre individus caractérisés par les axes
fig. 4 - Contribution des villes (individus)
sur le 1er plan factoriel
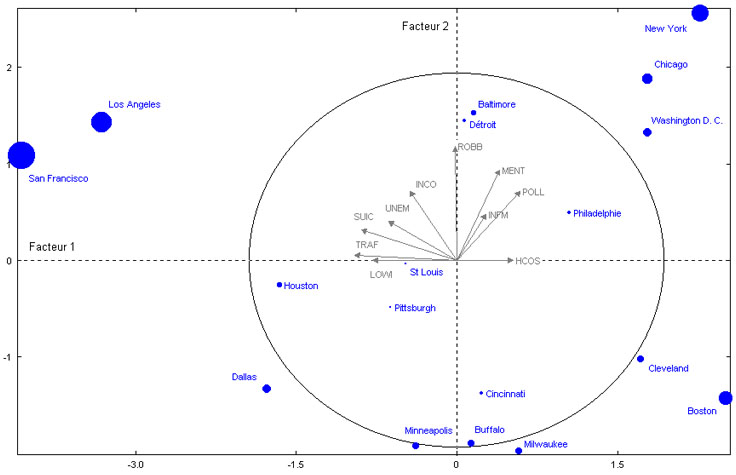
2.2.4.3. Par l'analyse graphique des qualité (Cos2)
- Modification
des Couleurs et symboles
- Double clic sur le graphique
- Présélections pour un nouveau graphique : individus
actifs
Valider par OK
- Menu Sélection
+ De tous les
points
- Menu Habillage
+ Ecrire les
libellés
- Menu Habillage
+ Couleurs et
symboles
Symboles = cercle
Couleur = rose
Taille proportionnelle = cos2
Valider par OK
- Paramétrage
de la proportionnalité
- Menu Dessin
+ Paramétrer la
proportionnalité
Taille minimale des symboles en pixels = 1
Taille maximale des symboles en pixels = 16
Ce paramétrage permet d'accentuer la
différence entre individus caractérisés par les axes
- Filtrage
statistique de la sélection
L'objectif est de restreindre la
sélection aux points réellement significatifs
Pour nous : la qualité (cos2)
- Menu Sélection
+ De tous les
points
- Menu Sélection
+ Filtrage statistique
de la sélection
Premier axe = axe 1
Deuxième axe = axe 2
Sélection du bouton cos2
Seuil en pourcentage de la valeur maximale = 50%
(correspond à 45°)
Ne seront représentées que les
villes qui ont un cos2 qui atteint ou dépasse 50 p.100 sur
un des axes (pas forcément celui du plan factoriel représenté).
Cliquer sur Calculer
indique 7 points sélectionnés
Valider par OK
- Mise
en évidence des points réellement retenus
- Menu Sélection
+ Inversion de la
sélection
- Menu Habillage
+ Mettre en
fantôme
- Menu Dessin
+ Rafraîchir
fig. 5 - Qualité (Cos2) des
villes (individus) 1er plan
factoriel
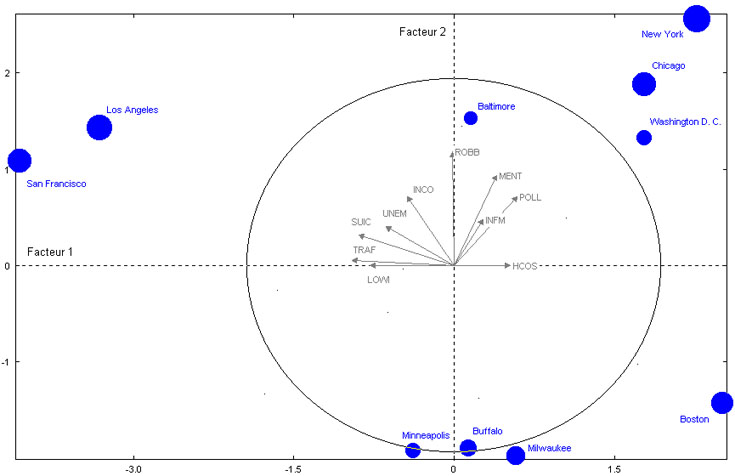
Ne sont donc représentées que
les villes qui ont un cos2 qui atteint ou dépasse 50 p.100 sur
un des axes (pas forcément celui du plan factoriel représenté).
On ne peut interpréter avec sécurité les proximités
entre les villes que si elles sont bien représentées sur le plan
factoriel.
C'est le cas, une fois les "fantômes" masqués.
- Ajouter du texte
Pour mettre un titre au graphique ou des
titres aux secteurs du plan factoriel
- Menu Dessin
+ Insérer un
texte
Cliquer avec la souris à l'endroit où vous souhaitez
insérer le texte
- Saisir le titre du graphique dans la fenêtre d'Édition de texte
Valider par OK
Il est possible de déplacer ou de modifier le texte
- Que faire si vous êtes "sec" pour
décrire les plans factoriels (les axes par les variables) ?
Allez lire les résultats de la procédure DEFAC
Vous y trouverez les deux variables qui "comptent",
axe par axe
- Changer les axes
Pour permettre l'analyse visuelles des
autres composantes
- Menu Graphique
+ Changer les
axes
- Choisir pour l'axe horizontal : axe 3
- Choisir pour l'axe vertical : axe 4
Le taux d'inertie sous chaque axe s'affiche
Valider par OK
Ce sont les textes du précédent plan factoriel qui
s'affichent :
- Faut-il les modifier ?
N'oubliez pas, à l'issue de chaque
analyse, de copier-coller dans votre traitement de textes les documents
réalisés. Ils vous permettront d'étayer votre développement, même en
l'absence du logiciel.
- Ne faudrait-il pas tester la même
analyse en mettant Los Angeles et San Francisco en individus
illustratifs ?
Refaire tourner une ACP en ce sens, à l'aide d'une
nouvelle filière, et comparer !
N'oubliez pas de revenir aux données brutes pour
l'analyse et le commentaire.
2.3. Cartographie des axes factoriels
-
Quelles discrétisations (variables visuelles) ont été retenues dans les
exemples suivants ?
- figurés
proportionnels ?
- montées en valeurs
?
- pourquoi ?
fig. 8 - Une possibilité de légende pour la
cartographie d'un axe factoriel (avec analyse)
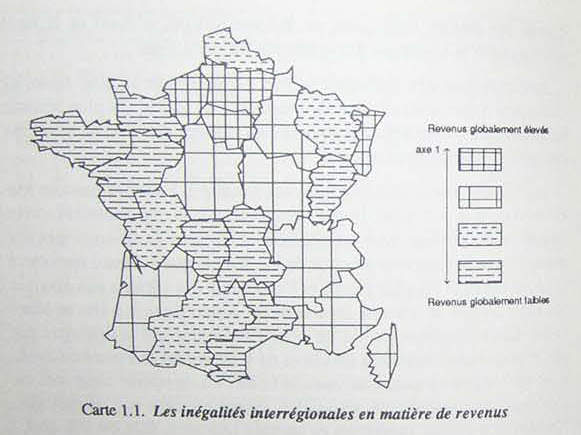
sources : SANDERS
1989, p. 76
fig. 9 - Une possibilité de légende pour la
cartographie de deux axes factoriels (avec analyse)
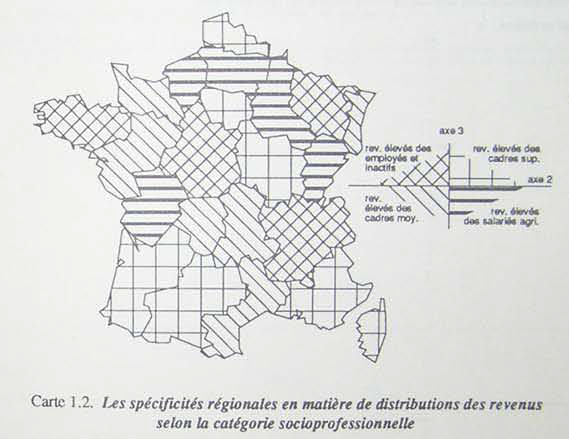
sources : SANDERS
1989, p. 77
fig. 10 - Autre possibilité de légende pour la
cartographie d'un axe factoriel (sans analyse)
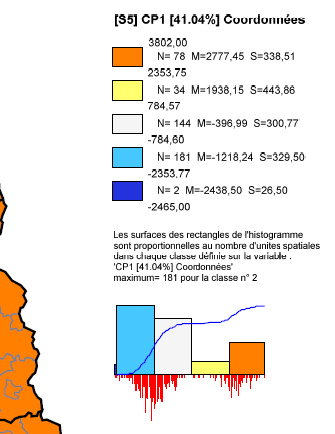
sources : WANIEZ
sd, p. 180
fig. 11 - Autre possibilité de légende pour la
cartographie d'un axe factoriel (sans analyse)
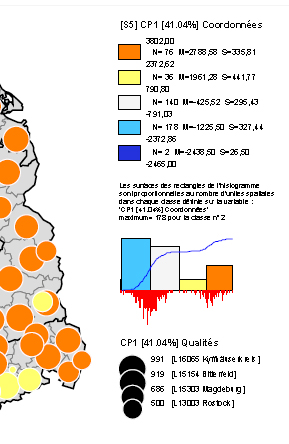
sources : WANIEZ
sd, p. 181
3. Analyse d'un 2e exemple
Exemple n°2 : Tableau 2.2 - Notations au 1er
semestre 2008-09
Téléchargement
du
fichier
Ce fichier est au format EXCEL 2003 et "pèse" 97 Ko.
Le choix de ces données repose, non sur l'intérêt intrinsèque qu'elles
représentent, mais sur la complexité de leur distribution statistique
(valeurs exceptionnelles, distribution non symétrique, etc.), ainsi que
par la gestion des données manquantes
qu'elles entraînent et la présence de données
nominales et continues illustratives.
L'objectif de cet exemple est de :
- comparer une analyse par ACP et par AFC d'un même
tableau
- voir comment combiner une variable nominale
illustrative et des continues actives et illustratives.
4. Analyse d'un ne exemple
Exemple n°3
: AMAT (J.-P.), GODARD (V.), HOTYAT (M.) - 2003 - Milieu, gestion,
histoire et scénarios de reconstitution dans les sylvosystèmes touchés
par les tempêtes de décembre 1999, GIP-ECOFOR, Min. agriculture, 115 p.
Analyse des dégâts tempétueux en Forêt
de Fontainebleau
Téléchargement
du
fichier brut
Ce fichier est au format texte tabulé et "pèse" 5 Ko.
Téléchargement
d'un
fichier résultat
Ce fichier est au format .xls et "pèse" 97 Ko.
Téléchargement
de
la carte des limites et points d'enquête
Ce fichier est au format .gif et "pèse" 386 Ko.
Téléchargement
du
rapport
Ce fichier est au format .pdf et "pèse" 4,5
Mo !!.
Exemple n°4
: Tableau 4.1 - La structure pastorale éthiopienne par awrajas (en
nombre de têtes), [Sources : EASTMAN
(J.R.) - 1997 - 10. Database Workshop. in : IDRISI for Windows.
Tutorial Exercises. Version 2.0. Worcester (MA, USA), Clark University,
pp. 69-79 et traduction française GODARD,
2003]
Téléchargement
du
fichier brut
Ce fichier est au format Excel (.xls) et "pèse" 51 Ko.
Téléchargement
du
fichier résultats
Ce fichier est au format Excel (.xls) et "pèse" 40 Ko.
Pour la cartographie de l'analyse :
- sous ArcGis, récupérer le
fichier de formes (shp) et sa base de données dans le dfm04ta1_ag.rar.
Ce fichier est compressé (.rar) et "pèse" 68 Ko.
Ce tableau est le support d'un exercice détaillé sur la fiche
guide 1.8 du cours de SIG.
Exemple n°5
: Évaluation de la vulnérabilité socio-économique
par rapport aux tempêtes extrêmes et aux inondations qui les
accompagnent (Revere, Massachusetts, USA)
Ce tableau est le support d'un exercice détaillé sur la fiche
guide 6.2 du cours de Master 2 recherche.
Téléchargement
du
fichier brut
Ce fichier est au format Excel (.xls) et "pèse" 46 Ko.
Téléchargement
du
fichier résultats
Ce fichier est au format Excel (.xls) et "pèse" 46 Ko.
Pour la cartographie de l'analyse :
- sous ArcGis, récupérer le
fichier de formes (shp) et sa base de données dans le revere.rar.
- sous Idrisi, s'inspirer du TD
de télédétection "mtd42tel.htm" et particulièrement du passage qui
traite de cartographie
(à la section 5.5 Cartographie des UEA ) et de l'enregistrement en
DBASE ".dbf" qui rend le fichier EXCEL directement importable dans
Idrisi.
fig. 6 - Les hispaniques dans les "blocs" de
recensement à Revere (Mas., USA)
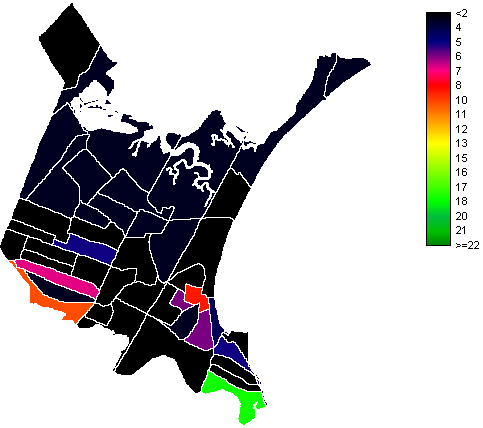
fig. 7 - Les pauvres dans les "blocs" de
recensement à Revere (Mas., USA)
Exemple n°6
: Les élections législatives et présidentielles de 2012 par
département
Accéder aux données d'un certain nombre d'élections (data.gouv.fr)
Accéder
au
fichier brut des élections législatives
Accéder
au
fichier élaboré des élections législatives
Pour décrypter les sigles des différents partis : Wikipédia
Accéder
au
fichier élaboré des élections présidentielles
Téléchargement
du
fichier de données (dfm01ta6c.csv)
Ce fichier est
au format CSV et "pèse" 11 Ko.
Téléchargement du script ACP_elecpres_v3d.R
Le fond cartographique des limites administratives en 96 départements
est accessible ici : http://julienas.ipt.univ-paris8.fr/vgodard/pub/enseigne/carto2/claroline/tdfm32/depart_90_96.rar
Exemple n°7
: Quelques équipements de santé en 2012 par département
Les données portent sur : les établissement qui accueillent des
urgences (urg) ; les maternités (mat) ; les pharmacies (pha) ; et les
laboratoires d'analyse (lab) pour 100 000 habitants.
Téléchargement
du
fichier
Exemple n°8 : Le
second tours des élections municipales de 2014 à Fontenay-sous-Bois
Accéder aux données
Données
Cartelec
Données électorales Merci à Amale ERRAMI pour la
collecte et la mise en forme
Exemple
n°9 : La propriété forestière en
France
Accéder aux données
Téléchargement du fichier
(cf. détails sur la plateforme
Moodle à la rubrique La
propriété forestière française en 2007)
Pour comprendre les transformations
effectuées sur les distributions de cet exemple, une relecture de ce
passage du cours de carto niveau 2 sur les Transformations de variables sera un plus !
Pour visualiser la forme des distributions
après transformations, téléchargement :
du script graph_asymetrie.R ;
des données transformées de la forêt
domaniale et des collectivités transfo2_PropFor19_v2.csv
Le fond cartographique des limites administratives en 90 ou 96
départements [l'Île-de-France, pour les données forestières, a été
regroupée en ÎdF ouest, 75+78+91+92+93+94+95). La Seine-et-Marne est
restée indépendante] est accessible ici : http://julienas.ipt.univ-paris8.fr/vgodard/pub/enseigne/carto2/claroline/tdfm32/depart_90_96.rar
Téléchargement du script ACP_propforlog.R
Affichage du résumé de ce script généré en R
Markdown : ACP_propforlog_v3.Rmd
(en html)
Affichage de l'aide à l'analyse Investigate(res.propfor.pca) inclus dans le R
Markdown ci-dessus.
Récapitulatif :
- Quelques soient les mises en formes retenues, ils faut
passer par les trois étapes suivantes :
- Déterminer le nombre d'axes
factoriels qui comptent
- Caractériser les axes avec les
variables
- Caractériser les individus avec
les axes
- Pour constituer la typologie, n'oubliez pas d'asseoir
votre commentaire sur les données du tableau d'origine (c'est plus
parlant que les données centrées réduites !)
Assurez-vous que :
- chaque groupe d'individus (voire chaque individu) est
qualifié ;
- toutes les variables ont été vues (elles ne sont pas
toutes forcément qualifiantes).
- Vous n'aurez jamais un résultat unique à l'issue d'une
ACP car, il dépend :
- des variables et individus que vous avez retenus ;
- de votre
interprétation des plans factoriels.
4. Test de compréhension
|
Communiquez-moi sur la plateforme Moodle, à
la rubrique "Questions de cours", les réponses aux questions suivantes :
Question n°2.1. Parmi les
expressions suivantes, y en a-t-il une ou plusieurs qui ne
caractérise(nt) pas une Analyse en composantes
principales (ACP) :
a) matrice d'information
|
d) valeur propre
|
b) matrice des covariances
|
e) standardisation
|
c) matrice des corrélations
|
f) contribution
|
Question n°2.2. Parmi les
mots clefs suivants, lesquels sont compatibles avec la métrique
d'une Analyse en composantes principales (ACP) :
a) distance du khi2
|
d) fréquence absolue
|
b) distance de Manhattan
|
e) pourcentages
|
c) fréquence relative
|
f) qualité
|
Question n°2.3. Quel(s)
indicateur(s) d'une Analyse en composantes principales (ACP)
permet(tent) de repérer les individus trop exceptionnels :
a) coordonnées
|
d) inertie relative
|
b) contributions
|
e) inertie totale
|
c) qualités (contributions relatives)
|
f) poids
|
|
Retour au début de la fiche Mémo
Fiche Mémo suivante
NB : les mots suivis de "*" font partie du
vocabulaire statistique, donc leur définition doit être connue.
Faites-vous un glossaire.









