Vincent GODARD

Département de Géographie

Université de Paris 8

V.3.0 - Dernière mise à jour : 28/10/2022

Fiche Mémo n°1 du cours d'analyse de données pour le Master 2 :

Présentation de l'analyse des données (spatiales) multivariées et du logiciel R

Note : mon précédent cours d'analyse de données multivariées devait beaucoup à l'ouvrage de Léna Sanders, maintenant épuisé (sauf en bibliothèques, mais téléchargeable ici). Celui-ci s'inspire, en plus, pour la forme et pour certains exemples de celui de Pierre Dumolard. Qu'ils soient ici tous les deux remerciés pour leur contribution (involontaire ;-) !)

1. L'analyse des données multivariées

Groupes de techniques permettant :

- de traiter simultanément un ensemble nombreux de variables ;

- de ne pas faire d'hypothèses contraignantes a priori (surtout vrai pour les techniques descriptives) ;

- de faire ressortir une structure latente, profonde, non immédiatement décelable ;

- de simplifier et d'organiser l'information.

1) Analyse spatiale des données ou analyse des données spatiales ?

Ici, on ne s'occupera qu'a posteriori des contraintes spatiales !

Par exemple :

1) réalisation d'une typologie

2) représentation cartographique de la typologie

3) analyse spatiale de sa répartition

2) Quid de la notion d'indépendance des données ?

 

2. Les 2 grandes familles d'analyse multivariable

La culture disciplinaire prime sur l'outil.

Cependant, pour révéler le contenu sous-jacent de vos données, il est préférable d'avoir fait un peu de (et compris l'intérêt de la) :

- statistique univariée, typiquement le cours de statistique de L2 et en particulier : "2. Les valeurs centrales" ; "3. Les paramètres de dispersion"

- statistique bivariée, typiquement le cours d'enquête de L3 et en particulier : les "5. Analyses bivariées" entre caractères qualitatifs, quali/quanti et quantitatifs.

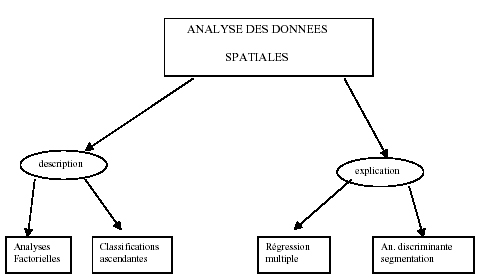
Ceci mis à part, deux grandes familles d'analyse multivariée sont abordées pendant ce cours :

- les analyses plutôt descriptives (ACP, AFC, classifications...)

- les analyses dites explicatives (régressions multiples, segmentations...)

fig. 1b - Les deux grandes familles d'analyse multivariée

Sources : Dumolard 2005, p. 3

- Parmi les méthodes descriptives (celles qui seront prioritairement pratiquées ici), on distingue deux grands groupes en fonction de leur finalité.

Ceux qui servent plutôt à :

- former des groupes de variables et à hiérarchiser l'information ;

=> analyses factorielles*

et ceux qui servent plutôt à :

- former des groupes d'individus ;

=> classifications multivariées*

- L'ensemble de ces méthodes est adapté à l'analyse de l'organisation de l'espace

- Ces méthodes nécessitent :

- une organisation de l'information géographique en matrice d'information spatiale* ;

- une réflexion sur le choix des unités spatiales élémentaires* (nature et échelle du problème traité) ;

- une réflexion sur le choix des variables* (homogénéité de l'information).

- Ces méthodes ne supposent pas :

- d'hypothèses sur la distribution statistique des variables (pour certains auteurs seulement ! Voir plus loin.) ;

- ni de connaissances de modèles probabilistes particuliers ;

contrairement aux méthodes classiques de la statistique.

- Quelles que soient les dimensions de la matrice d'information :

- Ces méthodes descriptives servent à :

- affiner les descriptions ;

- éliminer les "bruits" qui parasitent notre perception ;

- révéler les associations et les interactions ;

- éliminer la part d'arbitraire des comparaisons de cartes.

Donc à réaliser des typologies*

C'est à dire, constituer des groupes d'individus plus semblables entre eux qu'ils ne le sont avec les autres (au regard des variables étudiées).

3. La famille descriptive

3.1. Les analyses factorielles (en 2 mots lapidaires)

- Une analyse factorielle sert à :

- résumer ;

et

- hiérarchiser ;

l'information contenue dans un tableau numérique de :

- n lignes (les individus) ;

- p colonne (les variables).

Les n individus sont décrits par un nuage de points dans p plans [les p variables (soit p plans !)].

 Exemple :

Prenons les 20 arrondissements de Paris (n = 20 individus) et les recensements de 1990 et 1999 (p = 2 variables) ;

Le tableau de 20 lignes (1 par arrondissement) et deux colonnes (1 par recensement) sur un graphique à deux dimension formera un nuage de points de coordonnées x = population de l'arrondissement en 1990 et y = population de l'arrondissement en 1999.

 

3.1. Résumer l'information

- L'information représentée par ce nuage,

c'est la dispersion des n points.

- Produire un résumé de cette information c'est

projeter ces points dans un espace de dimension inférieure à p.

Exemple :

Prenons les 20 arrondissements de Paris (n individus) et les 33 recensements (p variables) ;

Cela donne un tableau de 660 "informations", soit 660 intersections possibles (20 * 33)

Pour l'analyser, il faut le résumer !

Passer de 33 variables à 2-3 néo-variables concentrant l'information d'origine serait une "bonne" opération cognitive !

C'est l'objectif de l'analyse multivariée

- Les axes de ce sous-espace sont dits "axes factoriels*" ou "facteurs*".

- Le résumé est possible dans la mesure où

les variables ne sont pas totalement indépendantes

- Chaque variable "p" porte en elle :

- une part d'information originale ;

- une part d'information redondante avec les autres.

C'est cette part d'information redondante que l'on va regrouper dans le résumé factoriel.

- Chaque facteur est la combinaison linéaire des "p" variables.

A chaque variable est associé un coefficient "a".

Ce coefficient "a" est proportionnel à l'intensité qui lie la variable au facteur.

Ces facteurs, ou axes, rendent compte des associations entre les variables.

Leur nombre apparaît bien plus réduit que celui des variables d'origine.

3.2. Hiérarchiser l'information

Les facteurs sont hiérarchisés :

- le 1^er axe concentre le maximum de l'information ;

- c'est l'axe de la plus grande dimension du nuage de points

- c'est le meilleur résumé dans un espace à une dimension

- mais il laisse des résidus (de l'information)

- le 2^e axe concentre le maximum de l'information restante ;

- il est orthogonal au premier (par construction)

- c'est l'axe de la plus grande dimension résiduelle du nuage de points

- associé au 1^er axe, c'est le meilleur résumé dans un espace à deux dimensions

- mais il laisse aussi des résidus

- le 3^e axe prend encore une part d'information moindre ;

- il est orthogonal au deux premiers (toujours par construction)

- ainsi de suite

3.3. Les grands types d'analyse factorielle

Objectif principal : former et hiérarchiser des groupes de variables

3.3.1 L'analyse en composantes principales (ACP)

C'est la technique la plus ancienne

- S'applique principalement aux tableaux de mesures*

=> variables quantitatives (données brutes, ratio, %, ...)

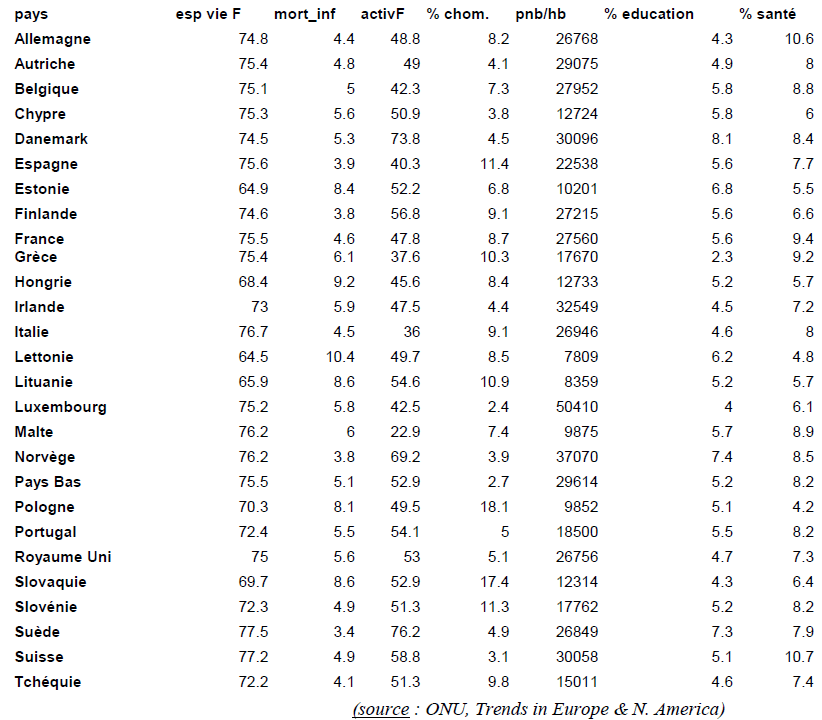
tab. 1 - Variables démographiques et économiques pour 27 pays européens (DUMOLARD 2005, tab. 2.2) => matrice d'information spatiale

3.3.2 l'Analyse factorielle des correspondances (AFC)

- S'applique principalement aux tableaux de contingence*

=> variables quantitatives (données brutes sommables en lignes et en colonnes)

- Mais également aux tableaux disjonctifs complets*

=> variables qualitatives (nominales en présence / absence)

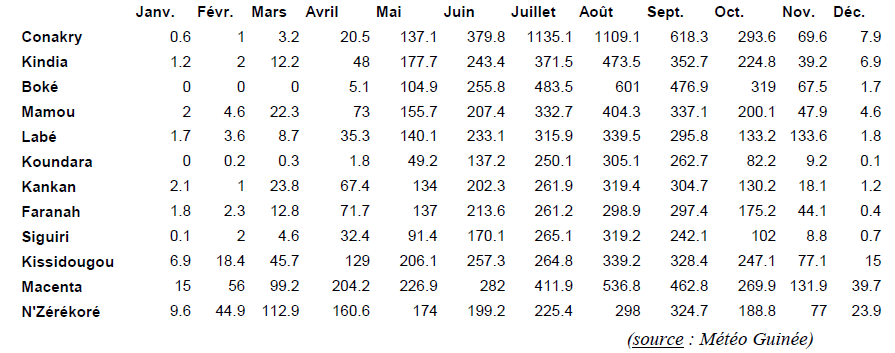
tab. 2 - Précipitations moyennes mensuelles de 12 villes guinéennes (DUMOLARD 2005, tab. 2.3) => matrice d'information spatio-chronologique

4. Les grands types de classification multivariée

Objectif principal : former des groupes d'individus

- Les classifications ascendantes hiérarchiques (CAH)

Une des techniques les plus utilisées en géographie.

Permet :

- d'effectuer des typologies emboîtées ;

puis

- des cartographies.

- Les classifications autour de centres mobiles, type nuées dynamiques

- Méthodes utilisées sur de très grosses populations

- Permet de rechercher le nombre de classes optimales le plus stable (robuste)

repose sur un grand nombre d'itérations

- Les classifications à limites mobiles ou floues

- Quand les classes obtenues :

- ne sont pas disjointes ;

- reposent sur des probabilités d'appartenance...

Ces deux dernières ne seront pas abordées ici.

Les analyses factorielles et les techniques de classification sont complémentaires.

On sera donc amené à les utiliser conjointement.

Elles permettent :

- de tester de nombreuses hypothèses,

mais n'ont aucun pouvoir explicatif !

- d'extraire successivement des résumés unidimensionnels indépendants et hiérarchisés dont l'importance informative (variance) est dégressive.

Ce sont des techniques exploratoires pour réduire la complexité initiale du tableau d'information.

4. La famille explicative (prédictive)

4.1. Les régressions linéaires

4.1.1 Régressions linéaires simples

4.1.2 Régressions linéaires multiples

4.2 Les autre régressions

En attendant que ces parties là soient rédigées, on consultera avec intérêt les liens suivants :

La régression logistique : https://perso.univ-rennes1.fr/valerie.monbet/ExposesM2/2013/La%20re%CC%81gression%20logistique.pdf

Régression logistique binaire, multinomiale et ordinale : http://larmarange.github.io/analyse-R/regression-logistique.html

 4.2.1 Régressions logistiques binaires

Introduction à la régression logistique : https://statistique-et-logiciel-r.com/regression-logistique/

 4.2.1 Régressions logistiques multiples

 5. R et les tests

La plupart des méthodes explicatives font appel à des tests de significativité : "cette variable est elle significativement explicative (je la retiens, ou pas ?) ?", etc.

Certaines méthodes descriptives aussi pour sélectionner les variables ou les individus qui "comptent" dans l'analyse.

En général, les géographes sont peu familiarisés, contrairement aux psychologues ou aux biologistes, aux questions de représentativité des échantillons.

Ce petit chapitre essaye de présenter quelques exemples utiles aux géographes pour en saisir les enjeux.

Une version plus développée est accessible ici Annexe 2, et là mem51enq.htm .

5.1. Comparaison d’une distribution observée avec une distribution théorique

Dit comme ça, cela semble loin de la géographie !

Eh pourtant !

Quand on souhaite répondre à la question : "y a-t-il eu progression du "mitage" par l'habitat dans les oliveraies du secteur de Volx (04) entre 1960 et 1990 ?", c'est bien ce que l'on va faire ! Les données suivantes sont issues d'un TP du cours d'enquête de L3 (cf. TP n°1 du cours d'enquête), où les étudiants échantillonnaient sous les intersections d'une grille "jetée" sur des photos aériennes (tirage systématique) pour savoir s'il y avait du bâti ou non sous chaque intersection à chaque date de prises de vues.

Cette distribution de points observés va être comparée à une distribution de points théoriques, celle que donnerait le hasard !

Si le semi de points bâtis est dû au hasard, alors il y a de grandes chances pour qu'il n'y ait pas de différences entre le bâti 1960 et le bâti 1990 ! Bref, que les distribution soient indépendantes !

C'est ce qu'on va voir (tester !).

- Comment fabrique-t-on le semi théorique ?

Les données brutes

Années \ Urbanisation	Bâti	Non Bâti	Total
1960	98	1182	1280
1990	96	624	720
Total	194	1806	2000

Les données théoriques dérivées

- Calcul de l'effectif théorique d'une case

(Total Ligne * Total Colonne) / Nb total d'unités stat = Effectif si indépendance entre bâti et année de prise de vue

Années \ Urbanisation	Bâti	Non Bâti	Total
1960	(194 x 1280) / 2000 = 124.16	(1806 x 1280) / 2000 = 1155.84	1280
1990	(194 x 720) / 2000 = 69.84	(1806 x 720) / 2000 = 650.16	720
Total	194	1806	2000

5.1.1. Significativité globale du lien

- Comment comparer les données observées et les données théorique ?

Par un indice pondéré comparant l'écart entre l'observé et le théorique.

 

5.1.2. Indice du Khi2

L'indice du , prononcer Khi2*, est dû à Karl Pearson (Mathématicien anglais, 1857 - 1936)

formule n°1 - (mem51enq.htm)

Avec :

o_i valeur de la case observée ;

c_i valeur de la case calculée ;

j étant égale à 4 pour 2 variables dichotomiques.

Calcul du Khi2 par cellule

Années \ Urbanisation	Bâti	Non Bâti	Total
1960	(98 - 124.16)^2 / 124.16 = 5.51	(1182 - 1155.84)^2 / 1155.84 = 0.59	6.10
1990	(96 - 69.84)^2 / 69.84 = 9.80	(624 - 650.16)^2 / 650.16 = 1.05	10.85
Total	15.31	1.64	16,96

Calcul de l'indice global par sommation des cellules :

= (98-124,16)²/ 124,16 + (1182-1155,84)²/ 1155,84 + (96-69,84)²/ 69,84 + (624-650,16)²/ 650,16 = 16,96

- Cet indice est-il suffisamment élevé pour conclure que date de prise de vue influe sur la présence du bâti ?

5.1.3. Test du Khi2

- Y a-t-il un lien suffisamment fort (dépendance) entre la date de prise de vue et la présence du bâti ?

En fait, on cherche plutôt à tester l'indépendance (l'absence de lien) entre les années d'enquête, les modalités de la variable X, et l'urbanisation, exprimée en bâti / non bâti, la variable Y, dans le secteur de Volx (04).

- 1^ère étape :

On pose H₀ : il y a indépendance entre la date de prise de vues (1960 ou 1990) et le bâti observé.

- 2^e étape :

On calcule la valeur V de l'écart à l'indépendance entre X et Y :

= (98-124,16)²/ 124,16 + (1182-1155,84)²/ 1155,84 + (96-69,84)²/ 69,84 + (624-650,16)²/ 650,16 = 16,96

- 3^e étape :

- On détermine la valeur seuil V'.

Comme V a été déterminée selon la métrique* du , la valeur-seuil V' est lue dans la table du (cf. Table n°1 ).

- pour un risque d'erreur fixé dans l'exemple = 0,05 ;

- pour un nombre de degrés de liberté (d.d.l.) (prononcer nu) :

formule n°2 - (mema1enq.htm)

Avec :

n nombre de modalités de la 1^ère variable (X) ;

p nombre de modalités de la 2^e variable (Y).

donc = 1

et V', lue dans la table vaut :

V' = 3,841

- 4^e étape :

- V est supérieure à V'

=> 16,888 > 3,841

H₀ est rejetée, on rejette l'indépendance entre la date de prise de vue et la densité du bâti à Volx.

En fait, on devrait dire : on rejette H₀ car il y a moins de 5 p.100 de chances (voire moins de 1 pour 1000) d'observer cet échantillon si H₀ est vraie ! Pour plus d'explication voir l'ouvrage de Denis POINSOT (POINSOT, 2004), en particulier la section "7.2 détail des étapes d'un test statistique"

Cette dépendance est même significative au seuil de 1 p.1 000 ( = 0,001)

- Dans la pratique, on peut supposer qu'il existe une relation entre X et Y.

5.2. Évaluer une dépendance entre deux variables quantitatives

Sources : Test de corrélation entre deux variables de STHDA

Utilisation d'un coefficient de corrélation :

• r de Bravais-Pearson (test paramétrique, cas d'une distribution normale) ;
• voir, à ce sujet, pour se rafraîchir la mémoire, ce passage dans la mem43tel.htm relatif à la notion de corrélation entre canaux satellitaux.
• tau de Kendall (test non paramétrique basé sur les rangs, cas d'une distribution non normale) ;
  
• rho de Spearman (test non paramétrique basé sur les rangs, cas d'une distribution non normale).
• voir, à ce sujet, pour se rafraîchir la mémoire, ce passage dans la mem53enq.htm relatif aux tests non paramétriques.

5.2.1 Test r de Bravais-Pearson

On souhaite répondre à la question : "La corrélation entre les variables UNEM (chômage) et SUIC (suicide) pour les 18 villes états-uniennes est-elle significative (cf. Matrice des corrélations du cours d'analyse de données en Master 2) ?"

- 1^ère étape :

On pose H₀ : il y a indépendance entre le chômage (X) et le suicide (Y).

- 2^e étape :

On lit la valeur V de l'écart à l'indépendance entre X et Y dans le tableau de la matrice des corrélations :

r = 0,64

- 3^e étape :

- La valeur-seuil V' est lue dans la table du coefficient de corrélation du r de Bravais-Pearson (cf. Table n°3 ).

- pour un risque d'erreur fixé, dans l'exemple = 0,05 ;

- pour un nombre de degrés de liberté (d.d.l.) (prononcer nu) :

= n - 2 = 18 - 2 = 16

et V', lue dans la table vaut :

V' = 0,4683

- 4^e étape :

- V est supérieure à V'

=> 0,64 > 0,47

H₀ est rejetée, il n'y a pas indépendance entre le chômage et le suicide pour ces 18 villes.

- On peut dire que :

- r diffère significativement de 0 au seuil de 5 % ;

- que H₀, l'hypothèse d'indépendance, doit être rejetée, avec le risque de 1^ère espèce < 0,05 %.

En fait, on devrait dire : on rejette H₀ car il y a moins de 5 p.100 de chances d'observer cet échantillon si H₀ est vraie ! Pour plus d'explication voir l'ouvrage de Denis POINSOT (POINSOT, 2004), en particulier la section "7.2 détail des étapes d'un test statistique"

- On peut même dire que :

- r diffère significativement de 0 au seuil de 1 %

- Dans la pratique, on peut supposer qu'il existe une relation entre X et Y.

Quand la relation n'est pas linéaire, ce qui est le cas ici, il est préférable de tester la corrélation des rangs de Kendall ou de Spearman.

et de comparer le coefficient obtenu avec celui lu dans la table du r de Bravais-Pearson (cf. Table n°3 ).

5.2.2 Test des rangs de Kendall et de Spearman

Il faut trier les valeurs de chacune des variables UNEM (chômage) et SUIC (suicide) puis leur attribuer le n° de leur rang à la place des valeurs et faire les tests sur les rangs (cf. le script R).

On regarde la p-value pour statuer sur l'indépendance ou non entre les variables.

5.3. Récapitulatif des tests possibles selon les cas de figure

Un site qui recense sans doute la plupart des cas de figures : XLSTAT  et son guide de choix des tests statistiques !

Certains sont spécialisés pour R, comme STHDA, mais nécessitent de savoir ce qu'on veut faire.