V.2.2 - Dernière mise à jour : 29/11/2022
- 1er cas de figure
- Les caractères sont :
- quantitatifs ;
- des entiers (décimaux sous certaines conditions !) ;
- tous positifs ;
- regroupés dans un tableau de contingences*
- Le tableau de contingences est constitué de :
- n individus statistiques ;
qui peuvent être des unités spatiales (tableau de données = tableau d'information géographique)
- p variables quantitatives.
Alors,
- il est possible d'effectuer sur ce tableau une Analyse des correspondances simples, ou binaires.
- 2e cas de figure
- Les caractères sont :
- qualitatifs ;
- des effectifs (fréquences absolues) ;
- tous positifs ;
- regroupés dans un tableau quelconque qui sera transformé en un tableau disjonctif complet* (dans certains cas appelé tableau logique)
- Le tableau disjonctif complet est constitué de :
- n individus statistiques ;
qui peuvent être des unités spatiales (tableau de données = tableau d'information géographique)
- p variables qualitatives.
Où chaque modalité des variables p :
- devient une "colonne" ;
- est codée en présence / absence (1 ou 0).
Alors,
- il est possible d'effectuer sur ce tableau une Analyse des correspondances multiples.
Comme l'ACP, l'AFC a pour but de hiérarchiser l'information contenue dans un tableau de données. Elle va aussi bien s'intéresser à l'étude des colonnes (variables) qu'à l'étude des lignes (individus) du tableau d'information pour confronter les différentes distributions et permettre :
- de découvrir des irrégularités dans ces distributions ;
- d'analyser des interrelations entre les variables ;
- de mettre en évidence des combinaisons plus ou moins systématiques entre les variables ;
En bref, de dégager des structures dans l'espace géographique étudié, qui ne sont pas forcément linéaires.
Cela passe par une simplification de l'information d'origine
L'AFC se pratique sur :
- des tableaux de contingences ;
ou
- des tableaux quelconques transformés en tableaux disjonctifs complets.
Contrairement à l'ACP, les calculs relèvent de la métrique
du khi deux* (noté
![]() )
)
- Qu'est-ce qu'un tableau de contingence ?
C'est un tableau constitué de nombres entiers où :
- la somme en lignes a un sens !
- la somme en colonnes a un sens !
tab. 1 - Superficie des types de peuplements en Picardie en 1984 (en ha)
Sources : Superficie en bois et forêts en 1984, Statistique agricole annuelle 1984, Ministère de l'Agriculture, SCEES
Feuillus Résineux Mixtes Total par dép. Aisne 106 500 3 380 1 470 111 350 Oise 101 700 10 000 0 111 700 Somme 45 200 4 350 50 49 600 Total Picardie 253 400 17 730 1 520 272 650
Faire une ACP ou une AFC, c'est chercher à établir des degrés :
- de ressemblance ;
et
- de différence entre les unités spatiales (ou les variables).
- Pourquoi ne pas garder la même métrique que dans l'ACP pour les peuplements forestiers de la Picardie ?
Si l'on choisit la distance euclidienne sur les données brutes pour mesurer ces différences entre départements, on obtient les écarts suivants :
d(Aisnes ; Oise)2 = (106 500 - 101 700)2 + (3 380 - 10 000)2 + (1 470 - 0)2 = 69 025 300
d(Aisnes ; Oise) = (69 025 300)1/2 = 8 308,1 ha
d(Aisnes ; Somme) = 61 324,1 ha
d(Oise ; Somme) = 56 781,8 ha
L'Aisnes et l'Oise se ressemblent alors que la Somme diffère.
Pourtant, sur le tableau 1 les profils de l'Oise et de la Somme, avec une forêt mixte très faible, sont très proches.
- Dans ce contexte, la distance euclidienne transcrit les différences de masse entre les départements :
L'Aisnes et l'Oise se ressemblent car leurs superficies sont proches.
- Pour éliminer l'artefact lié aux ordres de grandeur, il faut transformer les données :
en pourcentage, par exemple !
Mais attention, le tableau des pourcentages n'est plus un tableau de contingences.
tab. 2 - Part des types de peuplements en Picardie en 1984 (en %)
Sources : Superficie en bois et forêts en 1984, Statistique agricole annuelle 1984, Ministère de l'Agriculture, SCEES
Feuillus Résineux Mixtes Part du dép. dans la région Aisne 95,6 3,0 1,3 40,8 Oise 91,0 9,0 0,0 41,0 Somme 91,1 8,8 0,1 18,2
Si l'on choisit la distance euclidienne sur les données relatives pour mesurer ces différences entre départements, on obtient les écarts suivants :
d(Aisnes ; Oise)2 = (95,6 - 91,0)2 + (3 - 9)2 + (1,3 - 0)2 = 57,9
d(Aisnes ; Oise) = (57,9)1/2 = 7,6 %
d(Aisnes ; Somme) = 7,4%
d(Oise ; Somme) = 0,2%
Cette fois, l'Oise et la Somme apparaissent bien comme se ressemblant le plus avec leurs forêts mixtes pratiquement nulles.
Pour annuler l'effet de masse, il est également possible de pondérer les distances.
- Qu'est-ce qu'une distance pondérée ?
C'est, par exemple, une distance euclidienne entre les profils (les lignes) des individus ou chaque terme est pondéré par l'inverse du poids relatif de la variable (colonne) correspondante.
Dans les calculs de distance, cette pondération :
- renforce le poids des variables de masse faible ;
donc
- compense les différences de poids entre les variables.
Sa formulation est la suivante :
formule n°1 - (mem03dea.htm)
Avec :
tab. 3 - Notations du tableau de contingence (lecture horizontale des quotients)
j = 1 2 . j j' . p Somme en lignes i = 1 k 1 1 k 1 2
k 1 . 2 k 2 1
k 2 . .
i
k i j k i j'
k i . i'
k i' j
k i' . .
n
k n . Somme en colonnes k . 1 k . 2
k . j k . j'
k . .
Si l'on choisit la distance euclidienne pondérée sur les données brutes pour mesurer ces différences entre départements, on obtient les écarts suivants :
Ce fichier est au format Excel (.xls) et "pèse" 193 Ko.
d(Aisnes ; Oise) = (0,0543)1/2 = 0,30
d(Aisnes ; Somme) = 0,39
d(Oise ; Somme) = 0,02
Cette fois encore, l'Oise et la Somme apparaissent bien comme se ressemblant le plus.
Cette distance pondérée s'appelle la métrique* (ou distance) du
, prononcer Khi2*.
tab. 4 - Récapitulatif des distances entre les départements (individus) de Picardie
Dist. euclidienne sur données brutes Dist. euclidienne sur données relatives (%) Distance du d(Aisnes ; Oise) 8 308,1 0,076 0,23 d(Aisnes ; Somme) 61 324,1 0,074 0,22 d(Oise ; Somme) 56 781,8 0,002 0,01
Remarques :
- Il ne faut pas comparer les distances entre elles, mais la hiérarchie à l'intérieure d'une distance ;
- La distance euclidienne sur les données brutes peut ne traduire que des effets de masse ;
- En raison de la symétrie des pondérations que la métrique du
impose au tableau de contingence, cette distance pondérée peut aussi bien s'appliquer aux lignes (individus) qu'aux colonnes (variables).
Si l'on veut répondre à la question :
- Quels sont les traitements sylvicoles les plus proches en Picardie ?
Alors, la formule devient :
formule n°2 - (mem03dea.htm)
Avec :
tab. 3bis - Notations du tableau de contingence (lecture verticale des quotients)
j = 1 2 . j j' . p Somme en lignes i = 1 k 1 1 k 1 2
k 1 . 2 k 2 1
k 2 . .
i
k i j k i j'
k i . i'
k i' j
k i' . .
n
k n . Somme en colonnes k . 1 k . 2
k . j k . j'
k . .
La distance du ![]() repose sur la comparaison
de profils
repose sur la comparaison
de profils
=> la masse des individus est relativisée (mais pas annulée comme lors d'une ACP sur des pourcentages) ;
=> le découpage spatial est peu marqué ;
=> la symétrie entre lignes et colonnes est conservée.
Ils sont très proches de ceux d'une ACP.
Cependant,
il existe quelques différences d'interprétation remarquables dues :
- au nuage de point construit sur les profils (des ligne ou des colonnes) ;
- à la métrique du
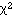
Mais, là encore,
on recherche les droites (les axes factoriels) d'allongement maximum du nuage de point
(celles qui sont les plus proches de tous les points simultanément)
- Chaque axe factoriel est défini par un vecteur dit
vecteur propre*
Les vecteurs propres définissent les différentes directions du nuage d'information
- La part d'information prise par chaque vecteur propre est appelée
valeur propre*
Elle définie la hiérarchie de l'axe factoriel.
- En AFC :
- la 1ère valeur propre est triviale, elle vaut 1 ;
elle ne sert pas à l'interprétation
- toutes les autres sont inférieures à 1 ;
- la plus grande d'entre-elles désigne la variance du 1er axe factoriel ;
- la 2e etc. ;
- la somme de toutes les valeurs propres mesure l'inertie totale du nuage.
- le degré de différenciation introduit par un axe est d'autant plus grand que sa valeur propre est élevée.
- Comme pour l'ACP :
- valeur propre = part de variance (d'information) du nuage prise en compte par l'axe
- elle est généralement exprimée en pourcentage
on parle indifféremment de pourcentages :
- d'inertie
- d'information
- de variance
- Cependant, contrairement à l'ACP :
- on étudie également les valeurs brutes des valeurs propres, car les 2 informations sont complémentaires :
- le taux d'inertie associé à une valeur propre permet l'analyse de la concentration de l'information sur l'axe ;
- la valeur brute permet l'analyse de la dispersion de l'information sur l'axe, donc la mesure de la différentiation spatiale (cas des tableaux d'information géographiques)
- les coordonnées, contributions ou qualités s'interprètent de la même façon
que l'on s'intéresse aux variables ou aux individus.
- indiquent les positions relatives des variables (ou celles des individus) :
- les unes par rapport aux autres ;
et
- par rapport au centre de gravité du nuage.
- contrairement à l'ACP, où ce sont des coefficients de corrélation.
Synonyme = contributions absolues*
- indiquent le rôle relatif des variables (ou celles des individus) :
- dans la formation (la caractérisation) ;
donc
- dans la dispersion ;
de l'axe factoriel
Elles permettent de repérer quelles sont les variables (ou les individus) les plus contributives par axe
- la somme des contributions vaut 1
- généralement exprimée en pour cent ou pour mille
Elles permettent :
- d'identifier les variables (ou les individus) qui définissent le mieux les axes ;
les plus contributives !
- Contrairement à l'ACP, deux variables (ou individus) peuvent être projetés au même endroit sur l'axe :
- avoir les mêmes coordonnées ;
- sans avoir les mêmes contributions.
Car la masse (cf. Poids relatif dans les tableaux d'analyse) de la variable (ou de l'individu) intervient dans le calcul de la contribution en AFC (cf. métrique du khi2).
C'est la différence de masses qui ferra la différence de contributions !
Donc, dans l'AFC, l'analyse des contributions revêt plus d'importance que dans l'ACP.
Synonyme = contributions relatives*
- permet de caractériser les variables (ou les individus) par les axes
- mesure la part de l'écartement d'une variable (ou d'un individu) au centre de gravité prise en compte par un axe
QLT = cos2 [de l'angle entre le vecteur-variable (ou individu) et l'axe]
cos2 (0°) = 1
=> variable (ou individu) sur l'axe
=> description parfaite de la variable (ou de l'individu) par l'axe
cos2 (90°) = 0
=> variable (ou individu) perpendiculaire à l'axe
=> description nulle de la variable (ou de l'individu) par l'axe
- généralement exprimée en pourcent ou pour mille
Ils complètent les indicateurs fournis pour chaque axe factoriel.
- La contribution* [ou Inertie relative*, INR(i)] de chaque variable (ou de chaque individu) à la dispersion du nuage de points.
=> s'obtient par le rapport de la distance de chaque variable (ou de chaque individu) au centre de gravité du nuage de points sur l'inertie totale du nuage de points.
formule n°3 - (mem03dea.htm)
Avec, ici dans le cadre du calcul de la contribution d'un individu :
INR(i) => inertie relative d'un individu i ;
fi. => sa fréquence ;
d2(i , G) => sa distance au centre de gravité, G, du nuage de points.
- une faible valeur pour la variable (ou l'individu) indique un profil proche du profil moyen ;
- une forte valeur pour la variable (ou l'individu) indique un profil caractéristique par rapport aux autres.
- La qualité* de représentation par rapport à l'ensemble des n 1er axes factoriels
=> s'obtient par l'addition de la qualité de chacun des n axes
Une faible valeur pour la variable (ou l'individu) indique un caractère marginal sur l'ensemble du nuage.
- La masse relative de chaque variable (ou de chaque individu).
- L'inertie totale*
=> s'obtient par l'addition de toutes les valeurs propres brutes
Lors d'études diachroniques (comparaison de recensements, ...), permet de voir si l'on va vers une homogénisation ou une spécialisation
- Quelles discrétisations (variables visuelles) ont été retenues dans les exemples suivants ?
- figurés proportionnels ?
- montées en valeurs ?
- pourquoi ?
fig. 1 - Une possibilité de légende pour la cartographie d'un axe factoriel (avec analyse)
sources : SANDERS 1989, p. 123
fig. 2 - Une possibilité de légende pour la cartographie de deux axes factoriels (avec analyse)
sources : SANDERS 1989, p. 124
fig. 3 - Autre possibilité de légende pour la cartographie d'un axe factoriel (écarts au profil moyen)
sources : SANDERS 1989, p. 121
Remarques :
L'ACP et l'AFC présentent des différences fondamentales, mais :
- bien souvent, c'est la nature des données et les objectifs qui font choisir l'une ou l'autre ;
- parfois, une simple transformation des données permet d'utiliser l'une ou l'autre.
Toutefois,
- si l'ACP ne se pratique que sur des données quantitatives ;
- l'AFC accepte :
- les données quantitatives ;
- les données qualitatives
mais les tableaux doivent être :
- de contingence
ou
- disjonctifs complets.
Exemple n°1 : Tableau 3.1 - La structure
socio-professionnelle des salariés (Pop Act en 1990) dans les régions
françaises (en nb d'emplois), (Sources : Céline ROZENBLAT "Les
salaires dans les régions françaises." Feuilles de Géographie, II-1994, Feuilles n°7, 10 p.)
Ce fichier est au format texte tabulé (.txt) et "pèse" 10 Ko.
Exemple n°2 : Tableau 3.2 - Le nombre de voies obtenues par les candidats aux élections présidentielles de 2002 (1er tour et 2e tour), (Sources : Conseil constitutionnel)
Ce fichier est au format texte tabulé (.txt) et "pèse" 15 Ko.
L'objectif de cet exemple est voir comment s'opèrent les regroupement et comment l'ajout de deux variables illustratives complète l'analyse.
Exemple n°3 : Tableau 3.3 - Surface en ha des différents postes d'occupation du sol issus de la base de données Corine Land Cover pour 156 communes de Côte-d'Or.
Ce fichier est au format texte tabulé (.txt) et "pèse" 15 Ko.
Exemple n°4 : Tableau 3.4 - La structure pastorale éthiopienne par awrajas (en nombre de têtes), [Sources : EASTMAN (J.R.) - 1997 - 10. Database Workshop. in : IDRISI for Windows. Tutorial Exercises. Version 2.0. Worcester (MA, USA), Clark University, pp. 69-79 et traduction française GODARD, 2003]
Ce fichier est au format Excel (.xls) et "pèse" 51 Ko.
Ce tableau est le support d'un exercice détaillé sur la fiche guide 1.8 du cours de SIG.
Téléchargement du fichier de données CSV (dfm04ta1.csv)
Ce fichier est au format CSV et "pèse" 11 Ko.
Téléchargement du script AFC_awrajas_v1.R
Pour la cartographie de l'analyse :
- sous ArcGis, récupérer le fichier de formes (shp) et sa base de données dans le dfm04ta1_ag.rar.
Ce fichier est compressé (.rar) et "pèse" 68 Ko.
Exemple n°5 : Tableau 3.5 - Somme des précipitations mensuelles de 72 villes françaises pour l'année 2010 (Sources : www.meteociel.fr)
Reconstitution de l'année 2010 (exemple de novembre) : http://www.meteociel.fr/climatologie/climato.php?mois=11&annee=2010
Ce fichier est au format texte (.csv). Les variables sont séparées par des ";" et "pèse" 6 Ko.
Affichage du résumé de ce script généré en R Markdown : AFC_precip_v3.Rmd (en html)
Affichage de l'aide à l'analyse Investigate(AFC_precip_v3_Investigate) inclus dans le R Markdown ci-dessus.
Exemple n°6 : Tableau 3.6 - Moyenne des températures maximales mensuelles de 72 villes françaises pour l'année 2010 (Sources : www.meteociel.fr)
Choix des températures
maximales pour ne pas avoir de moyennes négatives. Sinon, pour l'AFC,
faire un changement d'origine pour supprimer les valeurs négatives.
Reconstitution de l'année 2010 (exemple de novembre) : http://www.meteociel.fr/climatologie/climato.php?mois=11&annee=2010
Ce fichier est au format texte (.csv). Les variables sont séparées par des ";" et "pèse" 6 Ko.
- pour voir l'effet d'un outlier, remplacer la Tmax_dece pour Lanveoc par "329.7" (donnée avant correction) ;
- l'intitulé des variables qualitatives a été modifié pour une meilleure lisibilité.
tab. 3.6bis - Dictionnaire des variables qualitatives supplémentaires (illustratives)
RA Régions administratives RC Régions climatiques AURA Auvergne-Rhône-Alpes MED Climat méditerranéen BOFC Bourgogne-Franche-Compté MON Climat montagnard BRET Bretagne OAQ Climat océanique aquitain CEVL Centre-Val-de-Loire ODE Climat océanique dégradé CORS Corse ONO Climat océanique du nord-ouest GEST Grand-Est SCO Climat semi-continental IDFR Île-de-France HFRA Hauts-de-France NAQU Nouvelle-Aquitaine NORM Normandie OCCI Occitanie PACA Provence-Alpes-Côte-d'Azur PLOI Pays-de-Loire
Sources : Régions climatiques Climat_de_la_France (pages Wikipedia)
Affichage du résumé de ce script généré en R Markdown : AFC_Temperat_Max_v2.Rmd (en html)
Affichage de l'aide à l'analyse Investigate(AFC_Temperat_Max_v2_Investigate) inclus dans le R Markdown ci-dessus.
Exemple n°7 : Tableau 3.7 - Résultats du premier tours de la présidentielle de 2012, (Sources : regardscitoyens.org)
Ce fichier est au format Excel (.xls) et "pèse" 34 Ko.
Téléchargement du fond de carte
Ce fichier est compressé (.rar) et "pèse" 382 Ko.
Exemple n°8 : Tableau 3.8 - Élection présidentielle américaine de 2016, (Sources : Wikipedia.org)
Ce fichier est au format CSV (.csv) et "pèse" 3 Ko.
Affichage du résumé de ce script généré en R Markdown :
Récapitulatif :
Il n'est pas possible de dire que l'AFC est meilleure que l'ACP, et vice-versa.
On privilégie simplement une certaine forme d'entité de base lorsque l'on prend une méthode plutôt qu'une autre :
- c'est l'agrégat (département, région, ...) qui est privilégié par l'ACP sur les données en %.
- c'est l'individu (salarié, électeur, ...) qui est privilégié par l'AFC sur les données brutes.
Exemple n°5 : AMAT (J.-P.), GODARD (V.), HOTYAT (M.) - 2003 - Milieu, gestion, histoire et scénarios de reconstitution dans les sylvosystèmes touchés par les tempêtes de décembre 1999, GIP-ECOFOR, Min. agriculture, 115 p.
Analyse des dégâts en Forêt d'Armainvilliers
Téléchargement du fichier des données
Ce fichier est au format .xls et "pèse" 97 Ko.
Ce fichier est au format .pdf et "pèse" 4,5 Mo !!.
Analyse détaillé de l'exemple : voir la fiche pour SPAD 5.6
Exemple n°6 : porte sur le traitement et la représentation des risques majeurs dans le département de l'Aude en 2001. Il s'agit de coder les informations contenues dans le tableau synthétique des communes puis d'en faire une typologie et de la représenter sur un fond de carte communal.
Étape 1 => Entraînement à la manipulation d'ArcGIS
ou d'Idrisi à l'aide des 7 premiers exercices de prise en main ;
Étape 2 => Recodage des risques ;
- Téléchargement du Dossier départemental des risques majeurs ;
Ce fichier est au format .pdf et "pèse" 7,4 Mo.
Étape 3 => Import des fichiers des limites communales (format shape file, projection Lamber 2e) et du fichier des catastrophes naturelles ayant touché chaque commune (Sources Ministère de l'aménagement du territoire et de l'environnement, Préfecture de l'Aude, Dossier départemental des risques majeurs, 2001) ;
- Téléchargement du Couche communale du département de l'Aude et détail des catastrophes naturelles ;
Ce fichier est au format .zip et "pèse" 100 Ko.
Étape 4 => Préparation et traitement sous Excel des données scannées (merci PMK !)
- Téléchargement du tableau des données ;
Ce fichier est au format .xls et "pèse" 81 ko.
- Téléchargement du tableau des données recodées ;
Ce fichier est au format .xls et "pèse" 761 ko.
Étape 5 => Traitement sous SPAD et ArcGIS ou Idrisi des données scannées
- Téléchargement du tableau des résultats pour la partition en 5 classes ;
Ce fichier est au format .xls et "pèse" 108 ko.
|
Communiquez-moi sur la plateforme Moodle, à la rubrique "Questions de cours", les réponses aux questions suivantes :
Question n°3.1. Parmi les mots clefs suivants, le(s)quel(s) ne caractérise(nt) pas les données d'une Analyse factorielle des correspondances (AFC) :
Question n°3.2. Parmi les mots clefs suivants, lesquels sont compatibles avec la métrique d'une Analyse factorielle des correspondances (AFC) :
Question n°3.3. Quel(s) indicateur(s) d'une Analyse factorielle des correspondances (AFC) informe(nt) d'une évolution vers plus de différentiation dans les études multidates :
|
NB : les mots suivis de "*" font partie du vocabulaire statistique, donc leur définition doit être connue. Faites-vous un glossaire.